Gurobi10新功能：嵌入机器学习预测模型的优化问题

1 问题介绍

Gurobi10新版本已经发布了，其计算速度较上一个版本有了很大提升。当然新版本最让我个人感觉眼前一亮的是 Gurobi Machine Learning 这个新的算法包。这个新算法包对于研究和应用预测-决策问题的同学来说无疑是一个很好的工具。今天我们就来介绍预测-决策问题，并且以代码实例展示如何采用 Gurobi Machine Learning 算法包来求解这类问题。

常见的优化问题的形式：

其中  是决策变量， 表示可行域， 表示目标函数的系数。

上面就是一个很常见的优化问题的模型。当我们建立了上面的优化模型之后，若参数  是已知的，那么根据优化问题的不同类型我们可以设计出不同的算法来求解(1.1-1.2)问题。

然而在很多实际问题中参数  是未知的，此时我们就无法直接求解(1.1-1.2)优化问题。我们也经常把这样含有未知参数的优化问题称之为含有不确定参数的优化问题，这类问题也常采用随机规划，鲁棒优化，Online optimization 的方法来解决。本质上是一个预测-决策问题，预测问题解决的是不确定参数如何建模的问题，而决策问题解决的是在获得不确定参数后如何求解最优化的问题。

2 采用机器学习对优化问题不确定参数建模

得益于机器学习和人工智能的飞速发展，不同于传统的随机规划，鲁棒优化的方法，越来越多的研究者采用机器学习模型对不确定参数  进行预测。显然机器学习模型有着更加强大的模型表达能力，同时也对非线性包含复杂机理的问题有着很好的拟合能力。这一范式被称为嵌入机器学习模型的不确定参数优化问题，如下图所示

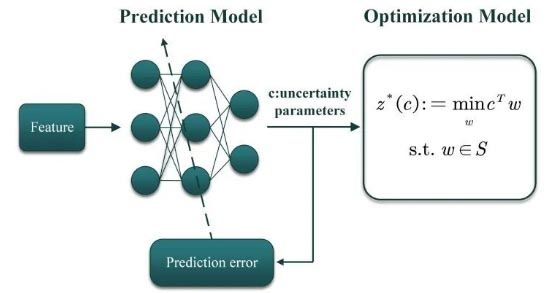
在上图中本质上是一个 两阶段法，在第一个阶段（Prediction Model）我们是采用机器学习算法对不确定参数  进行拟合，在第二阶段（Optimization Model）我们是采用机器学习模型预测的结果输入到我们的优化模型中，此时我们的优化模型就变成了确定性的优化问题，可以被直接求解。

我们把整个模型写下来：

其中函数 就表示预测模型，这个预测模型可以是有线性回归得到的，也可以是由神经网络得到，也可以是由决策树得到的，总之它可以代表任意一个预测模型。这个预测模型在第一个阶段已经得到了，在式(2.3)中这个模型是已知的，这个模型的参数是  自然也是已知的。

之前我们提到了由于 是一个不确定参数，所以我们会用这个预测模型 来预测得到这个不确定参数，自然 就是 feature 也就是输入，输出就是我们对不确定参数 的预测值。

观察式(2.1-2.3)所构成的优化问题，我们发现由于引入了预测模型，所以多了一个约束就是(2.3)，这个约束是一个比较奇葩一点的约束，它有点类似于一个黑箱模型。这个约束的输入输出映射关系是由一个复杂的预测模型所决定的，如果我们选择神经网络作为 的话，那么就可以知道这个约束(2.3)是一大堆非线性非凸函数的复合在一起的表达式。相比于原来的优化问题(1.1-1.2)，上述新的优化问题(2.1-2.3)由于包含的复杂的预测模型就会导致其求解非常困难。接下来我们在下一节中介绍如何在Gurobi Machine Leanrning 算法包中求解上述优化问题。

3 Gurobi Machine Learning 算法包代码实例

在前不久 Gurobi 10 新版本发布的时候，同时 Gurobi 也发布了一个 Gurobi Machine Leanring 算法包。Gurobi Machine Leanring 算法包 允许在优化问题中嵌入已经训练的好的机器学习模型作为约束条件。这实际上就是我们(2.1-2.3)所遇到的问题。

为了方便我们代码实例的展开，我们将式(2.1-2.3)的一般形式的优化问题具体化为一个目标函数包含不确定参数的指派问题。其模型如下所示：

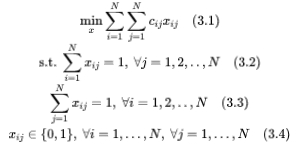
式(3.1-3.4)就是一个常规的指派问题，现在我们指定目标函数系数  是不确定参数，那么不确定参数是由如下的机器学习模型  g得到的：

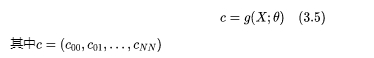
那么整个式(3.1-3.5)构成了嵌入机器学习模型的优化问题，接下来我们用在python代码调用 Gurobi Machine Learning 算法包来求解上述问题。

from sklearn.datasets import make_regression

from sklearn.metrics import mean_squared_error

from sklearn.neural_network import MLPRegressor

import numpy as np

import gurobipy as gp

from gurobi_ml import add_predictor_constr

from gurobipy import GRB

  

n_features, n_targets = 10, 4 # 机器学习模型输入维数和输出维数

X, y = make_regression(n_features=n_features, n_samples = 3000, n_targets = n_targets, noise=1.0) # 生成机器学习训练所需数据

pred_model = MLPRegressor([30, 20], max_iter=10000, random_state=1) # 建立神经网络

pred_model.fit(X, y) # 训练神经网络

# 随机抽取一个X和y

index = np.random.choice(X.shape[0], 1, replace=False)

X_examples = X[index, :]

y_examples = y[index, :]

n = 2 # 指派问题的规模大小

assert(n**2 == n_targets)

optim_model = gp.Model()

x = optim_model.addVars(n, n, vtype = GRB.BINARY) # 添加决策变量 x

optim_model.addConstrs(gp.quicksum(x[i,j] for i in range(n)) == 1 for j in range(n)) # 添加约束(3.2)

optim_model.addConstrs(gp.quicksum(x[i,j] for j in range(n)) == 1 for i in range(n)) # 添加约束(3.3)

input_vars = optim_model.addMVar(X_examples.shape, lb=X_examples, ub=X_examples) # 预测模型输入变量

output_vars = optim_model.addMVar(y_examples.shape, lb=-gp.GRB.INFINITY, ub=gp.GRB.INFINITY)# 预测模型输出变量

pred_constr = add_predictor_constr(optim_model, pred_model, input_vars, output_vars) # 添加约束(3.5)

pred_constr.print_stats()

obj = gp.quicksum(output_vars[0,i]*x[i//n, i%n] for i in range(n**2)) # 设置目标函数

optim_model.setObjective(obj)

optim_model.optimize()

optim_model.write("model.lp")

x_vars = np.array([optim_model.getVars()[i].x for i in range(n**2)]).reshape((n,n))

print("-------------------------------------------------------")

print("*** predict then optimze ***")

print("prediction output: {}".format(output_vars.X))

print("actual output: {} ".format(y_examples))

如下所示是最终求解结果：

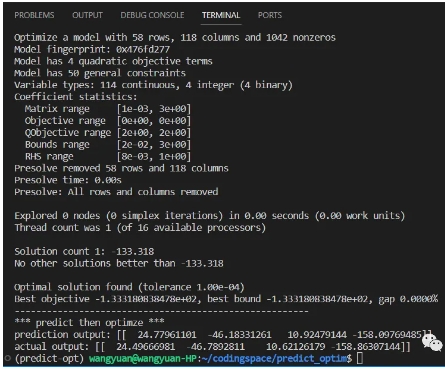
我们发现通过 Gurobi Machine Learning 可以非常方便的将 已经训练好的机器学习模型放入到优化问题中去，非常方便的可以实现从预测到决策的完整流程。机器学习和运筹优化两大范式在这个框架下可以结合起来。除了上面例子中演示的 scikit-learn 以外，Gurobi Machine Learning 也支持 pytorch 和 tensorflow 来作为预测模型。

4 Gurobi Machine Learning 安装

在安装 Gurobi Machine Learning 需要先安装如下算法包：

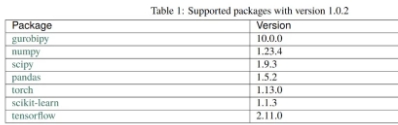
对于Gurobipy 的版本必须是10.0.0 才行。Numpy, Pandas 和 Scipy 三个算法包 采用 conda 或者 pip 安装即可。torch, scikit-learn, tensorflow 三个算法包 可以选装1-3个，这个主要是看你的预测模型是用哪个算法包搭建的就安装哪些算法包即可。

以上预安装算法包都安装完成后，可以用pip安装  Gurobi Machine Learning ：pip install gurobi-machinelearning

如下图是安装完毕后的结果：

上一条：Gurobi加速混合整数规划问题求解速度的建议

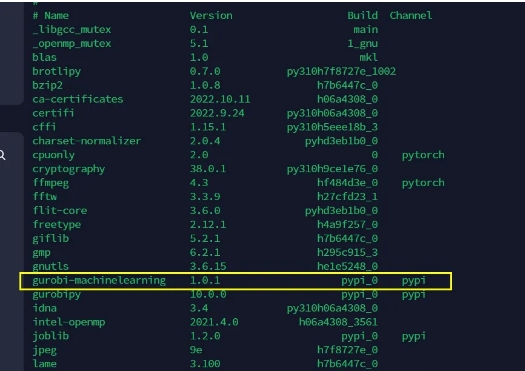
下一条：Anaconda常用指令