在做运筹优化的过程中,很多人会遇到一个问题就是自己建立好了模型,然后把模型导入到了求解器中,例如 Cplex 或者 Gurobi 等,就会发现求解器的求解速度很慢无法满足自己的要求。因此我将之前 Gurobi 官方给出的一些关于混合整数规划问题 依托于 Gurobi 求解器的加速技巧整理汇总并加入自己的理解放到这里,方便大家采用。
1 Gurobi 加速MIP求解速度的建议
1.1 模型建立
严格来说模型建立并不属于求解的范畴,但是一个好的模型会大大加速求解。可以说模型结构是内因,是导致速度的最主要因素。建模本身就是一种艺术,也很难有一套很标准化的方法来建模,更多的还是依赖长期的经验积累。所以说当你把你的模型导入到求解器中求解的时候,一定要区分清楚到底是因为模型建立不合理导致的求解慢,还是纯粹因为模型比较大求解慢。这个时候你可以先从一些小规模问题开始求解,如果小规模问题求解还比较慢,大概率说明建立的模型质量比较差,应该把主要精力放在建模上。
1.2 避免数值问题,不要出现过大过小系数
数值问题是求解器中经常会遇到的一个问题,也是大家经常忽视的一个问题。这个问题可以从Gurobi的日志文件中观察得到,如下所示:

如上所示就是Gurobi的日志,Matrix range 指的就是 约束矩阵系数的范围,从上面可以看到最小1e-13,最大是1e+15,不难看出这个数量级之间的差距是非常大的,这样的情况就容易导致数值问题,造成问题求解的困难。所以大家一定要注意观察日志文件关于系数范围输出的情况。
接下来简单分析一下两种比较简单系数过大或者过小的情况:
对于以下三个约束:
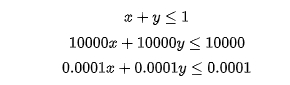
以上三个约束从数学上来讲是完全等价的,但是第一种约束的形式更利于求解器的求解,所以大家应该尽量避免第二种和第三种情况。
考虑以下约束:
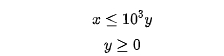
这类约束其实经常出现在采用大M法建模的问题中, 就有可能是一个大M,这就导致整个约束之间系数的数量级差别很大。那么为了避免这种情况可以将上述约束转化为如下等价形式:
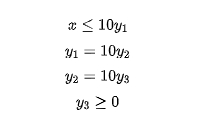
通过引入中间变量引入新的约束可以使得过大的系数被缩小。更多关于数值问题的说明和解决方法可以参考:
1.3 设置 NoRelHeurTime 参数,在Root Node之前获得可行解
对于大规模混合整数问题,可以尝试 NoRelHeurTime 参数。NoRelHeurTime 是控制 NoRel heuristic 算法调用时间的参数,在Gurobi里边默认是设置为0的。NoRel heuristic 算法应该(个人猜测)是一种LP-free primal heuristic 算法,它可以在Root Node之前获得可行解,对于算法之后的搜索很有帮助,尤其是对于大规模混合整数线性规划问题,提前拿到第一个可行解是非常非常有助于整个Branch and cut 的搜索过程的。
1.4 设置 MinRelNodes 参数,在Root Node获得可行解
Minimum relaxation heuristic 是一种非常耗时的启发式算法,同时其获得的可行解的质量一般比较差。因此如果其它启发式算法可以获得可行解的情况下一般不考虑调用 Minimum relaxation heuristic,如果其它启发式算法很难获得可行解可以考虑开启 Minimum relaxation heuristic,开启方法就是设置 MinRelNodes 参数(设置一个较大的数值,例如 10000)。
1.5 尝试Gurobi 参数自动调优功能
Gurobi 有参数自动调优的功能,可以自动寻找更好的优化参数。读入模型之后,清除已经设置的参数:m.resetParams(),然后设置自动调优的时间:m.Params.TuneTimeLimit = XXX (以秒为单位) 最后运行调优工具:m.tune()
1.6 尽量给每个变量设置一个紧的上下界
尤其在求解混合整数线性规划问题的时候,在添加决策变量的时候尽量都给每个变量设置一个上下界,因为在实际问题中大多数情况下变量值都是有界的。设置合理的上下界非常有利于求解器在内部的加速。
有些同学经常采用缺省参数的方法,不明确指定上下界,例如这样:m.addVar(x, ub= 100, vtype = GRB.Integer) m.addVar(x, lb = -1, vtype = GRB.Integer)
在Gurobi中如果缺省了参数lb(下界)的话,一般默认设为0,如果缺省了参数ub(上界)的话,一般默认设为正无穷。因此一定一定要注意,这些默认值可能和你原本模型设置不同,因此非常建议在 addVar的时候手动显式的添加一个合理的上下界,这样既不容易让程序产生Bug,也有利于求解器的加速。
1.7 合并非凸二次项
对于非凸二次,尽量通过合并的方式,增加线性项的数量,减少二次项的数量。例如ax² + bxy + cxz 这里面有三个二次项如果新定义一个变量 w=ax+by+cz,那么上面的表达式就成为xw 只有一个二次项。
1.8 调整 MIPFocus 参数
MIPFocus = 1: 侧重于优先找到一个可行解,MIPFocus = 2 侧重于问题的最优性,MIPFocus =3 侧重于问题的界。
1.9 Lazy cut
较难的约束可以采用 lazy 惰性约束,或者放在 callback 回调中进行判断。
2 Gurobi 提速小贴士 -- 零(无)目标优化
如果模型比较庞大,目标表达式比较复杂,Gurobi 找到第一个可行解花费了很长时间,那么可以尝试零目标优化的二种方法,看看能否帮助提速。零目标就是设置模型的目标函数为0,也就是 model.setObjective(0),替换掉之前复杂的目标。因为模型是否可行与目标无关,这样求解器可以专注在寻找第一个可行解上。当寻找到第一个可行解后,零目标模型自动结束优化。然后恢复到原来目标继续优化,那么就可以在第一个可行解基础上不断改进,有可能会加快优化速度。
因此,第一种做法,就是在程序中实现上面的步骤,优化分二步进行,调用二次 model.optimize() 函数。第二种做法,设置 ZeroObjNodes 参数,例如设置为 1000,那么当 MIP 模型完成根节点搜索后仍然无法找到可行解时,会启动 ZeroObj 算法,搜索可行解,直到达到设定的节点数,然后再进入到分支定界阶段。这个参数对于在根节点搜索中已经找到可行解的模型无效。
3 Gurobi 加速 Gap 收敛的方法
Gurobi 的优化 gap 的定义是 (当前可行解 - 当前松弛边界)的绝对值除以 当前可行解的绝对值。造成 gap 收敛慢的原因,有可能是可行解搜索速度较慢,也有可能是最优解或次优解已经找到,但松弛边界收敛慢造成证明最优性较慢。因此,用户可以通过加快找到可行解,以及加快松弛边界(用于证明当前可行解是否是最优解)二个方面入手。用户可以观察日志文件,看看 Objective Bounds 这部分 Incumbent 和 BestBd 这二列的变化。如果 Incumbent 收敛慢,有可能是最优解已经找到,也有可能是可行解搜索困难。用户可以通过调整优化参数和调整模型结构来加快速度,请参考群公告 【Gurobi 加速MIP求解速度的建议】 。如果 BestBd 变化缓慢,往往意味着松弛解和整数最优解的距离较远,可行域过于宽松,用户可以通过限制变量取值范围,添加额外约束,在callback 中添加自己的切平面等方式来改进。请参考群公告 【Gurobi 英文讲座资料】数学规划模型如何由弱变强。同时提醒用户,如果 BestBd 一列为0 时,会造成无论可行解是多少,按照定义,gap 都会是 100% 的情况,这种情况下,可以给目标函数增加一个常数定值,让目标远离数值0。
上一条:10个关于Docker的误解
下一条:Gurobi历史

品质保证
多年的生产力软件专家

专业实力
资深技术支持项目实施团队

安全无忧
多位认证安全工程师

多元服务
软件提供方案整合,项目咨询实施