Gurobi优化求解器中的约束矩阵的存储格式

优化问题中约束矩阵分析

思考这样一个问题，如下的混合整数线性规划问题：

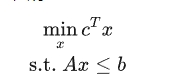
在上述问题中，涉及到优化问题的参数的主要是以下三个部分：

目标函数系数的向量：

约束右端项：

约束矩阵：

由于目标函数系数向量和约束右端项都是比较简单的向量，我们这里就不再赘述了。我们本篇文章主要讲一下约束矩阵  在求解器中是如何存储的，当然也可以理解为这是一个数据结构的问题。

想象一下，如果我们就按照正常矩阵的存储方式去存储约束矩阵  的话就会出现一个问题就是当 约束数量  和  变量数量  稍微大一点的时候，约束矩阵  所需要占据的内存将会是现在的计算机无法承受的。

比方说考虑约束为10万，变量也为10万的优化问题，那么  ,  ，我们假设约束矩阵的元素都是 double 类型的，进一步可得约束矩阵  所占内存大小为：

内存大小=元素数量×每个元素的大小

内存大小=10,000,000,000×8 字节内存大小=10,000,000,000×8字节

内存大小=80,000,000,000 字节内存大小=80,000,000,000字节

将字节转换为兆字节（GB）：

80,000,000,000 字节÷(1024×1024×1024)≈74.5 GB

所以，约束矩阵  大约需要占用 74.5 GB 的内存。显然约束10万变量10万的问题还算不上是大规模的问题，而仅仅只是保存这样一个约束矩阵  就需要这么多的内存，这显然是不现实的。

那么我们在优化求解器中肯定不会是老老实实的按照正常矩阵的存储方式来存储约束矩阵。我们很容易知道，约束矩阵  一般来说是非常稀疏的，也就是说约束矩阵 绝大部分元素都是0，非零元素是很少的。

我们如果按照正常稠密矩阵的存储方式会保存很多0元素，这无疑就是一种浪费。在优化求解器中我们一般是采用稀疏矩阵来保存约束矩阵  ，因为这样可以大大降低所需内存。接下来我们介绍主要在优化求解器中常用的两种存储约束矩阵的格式。

优化求解器中常用的稀疏矩阵格式

求解器中最常见的用来保存约束矩阵的稀疏格式是CSR（Compressed Sparse Row，压缩稀疏行）和CSC（Compressed Sparse Column，压缩稀疏列）。这两种格式通过只存储非零元素及其位置来实现节省内存空间的目的，下面我们分别来介绍

CSR (Compressed Sparse Row)

在CSR格式中，一个稀疏矩阵由三个数组表示：

values：这是一个一维数组，包含所有非零元素的值，按照行主序排列。

columns：这是一个与values同样长度的一维数组，记录每个非零元素在其所在行中的列索引。

row_ptr：这是一个长度为n+1的一维数组，其中n是矩阵的行数。它指示了每行非零元素在values数组中的起始位置和结束位置。特别地，第i行的非零元素位于values[row_ptr[i]:row_ptr[i+1]]之间。

以下通过一个例子来说明CSR矩阵，假设我们有一个如下所示的4乘4的矩阵：

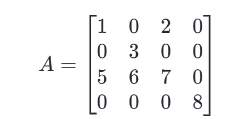
用CSR矩阵存储：

values: [1, 2, 3, 5, 6, 7, 8]

columns: [0, 2, 1, 0, 1, 2, 3]

row_ptr: [0, 2, 3, 6, 7]

从以上的例子我们可以看出采用CSR矩阵来保存约束矩阵  的时候，其所占内存大小和约束矩阵非零元素大小成正比。如果约束矩阵 是一个稀疏矩阵，显然采用CSR矩阵相比于稠密矩阵的存储方式来说会节省很多内存。

CSC (Compressed Sparse Column)

CSC格式与CSR格式相似，但是它是基于列的。一个稀疏矩阵在CSC格式下也是用三个数组表示：

values：同样是一个一维数组，包含了所有非零元素的值，但这次是按照列主序排列。

rows：这个数组记录了每个非零元素在其所在列中的行索引。

col_ptr：类似于CSR中的row_ptr，不过这次是指示每列非零元素在values数组中的起始位置和结束位置。第j列的非零元素位于values[col_ptr[j]:col_ptr[j+1]]之间。

以下通过一个例子来说明CSC矩阵，假设我们有一个如下所示的4乘4的矩阵：

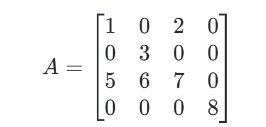
用CSC矩阵存储：

values: [1, 5, 3, 6, 2, 7, 8]

rows: [0, 2, 1, 2, 0, 2, 3]

col_ptr: [0, 2, 4, 6, 7]

从以上的例子我们可以看出采用CSC矩阵来保存约束矩阵  的时候，其所占内存大小和约束矩阵非零元素大小成正比。如果约束矩阵 是一个稀疏矩阵，显然采用CSC矩阵相比于稠密矩阵的存储方式来说会节省很多内存。

优缺点对比

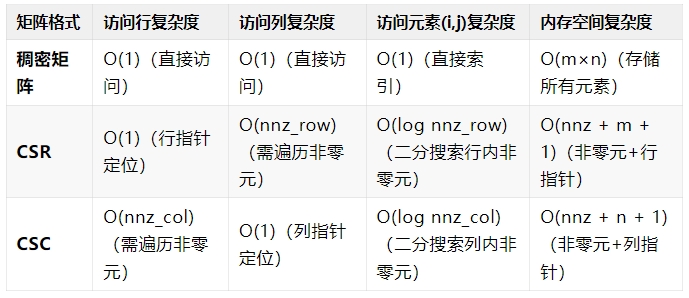
当然采用稀疏矩阵的格式来存储矩阵确实可以达到节省内存空间的效果，但这并不是没有代价的。稀疏矩阵的格式相对于稠密矩阵而言在访问矩阵内元素的时候需要额外的一些计算量。以下是一个对比：

符号解释：

nnz：矩阵中非零元素的总数。

nnz_row：某一行中的非零元素数量。

nnz_col：某一列中的非零元素数量。

CSR/CSC访问元素时，假设对非零元索引进行二分搜索（需有序存储），若无序则为 O(nnz_row) 或 O(nnz_col)。

如表格所示CSR格式在访问行的时候和稠密矩阵是一样的，但是访问列的时候复杂度就较高，同样的CSC矩阵在访问列的时候和稠密矩阵是一样的，但是访问行的时候复杂度就较高。所以我们需要根据实际应用场景来选择最合适的稀疏矩阵的格式。

Gurobi求解器中如何获取约束矩阵

在 Gurobi python 中可以采用 getA() 函数来直接获取优化问题约束矩阵，并且这个约束矩阵就是 CSR 格式的。示例代码如下：

model = gp.Model()

A_constrs = model.getA() # csr format

如果你想使用这个约束矩阵  你还需要在python中安装 Scipy 来辅助对这个矩阵进行操作。因为在python中这个约束矩阵的数据结构是借助了 Scipy.sparse 里边的CSR矩阵来定义的。目前在C++和Java API中似乎还没有同样功能的API函数。

上一条：Docker安装nginx

下一条：chemdraw软件官方介绍