Minitab 在质量控制工具中的应用

      质量控制工具是质量管理过程中重要的组成部分，其可帮助人们发现质量管理过程中存在的主要问题，从而改进过程。常用的质量控制工具包括控制图、柏拉图、鱼骨图、多变异图及对称图等。

一、控制图

        所有过程都会发生变异，过程变异可分为常规原因变异和特殊原因变异。常规原因变异是过程变异的正常部分，当只有常规原因影响过程输出时，表明过程受控制；特殊原因变异由系统外的原因造成，属于非随机变异。

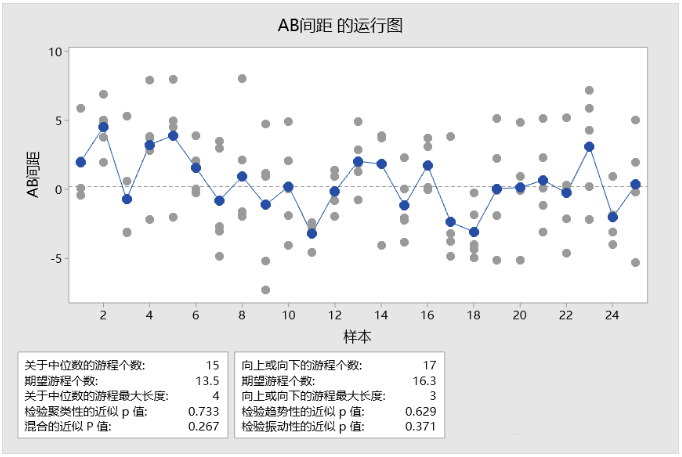
       图形中的灰色圆点原始测量值，而带有连线的蓝色圆点为自组均值。其下方提供以下两个随机性检验：

（一）中位数游程数检验

       该检验是基于中位数上下发生的总游程。游程为位于中位数同一侧的1个或多个连续的点，如果用连线将这些点连接起来，则当连线穿过中位数时，表示该游程结束，新的游程将从下一个点开始。下图展示15个游程及其游程最大长度。该检验可检验聚集和混合两种非随机行为：当观测游程数大于期望游程数时，表明数据为来自两个总体的混合数据；当观测游程数小于期望游程数时，表明数据存在聚集。但在图中，显示聚集 p = 0.733，混合 p = 0.267，均 ＞ 0.05 ，表明尚不能认为观测值存在混合和聚集的非随机行为。

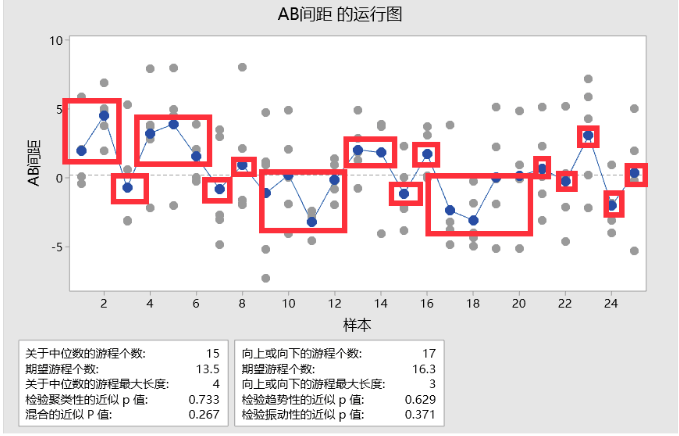
（二）向上或向下游程数检验

        该检验基于向上或向下的游程数。在此检验中，游程为相同方向1个或多个连续的点，每当数据序列出现方向变化时，将开始一个新的游程。该检验可检验趋势和振动两种非随机行为：当观测游程数小于期望游程数时，表明数据存在趋势的非随机行为；当观测游程数大于期望游程数时，表明数据存在振动的非随机行为；但在图中，显示趋势 p = 0.629，振动 p = 0.371，均 ＞ 0.05 ，表明尚不能认为观测值存在趋势和振动的非随机行为。

（三）操作步骤

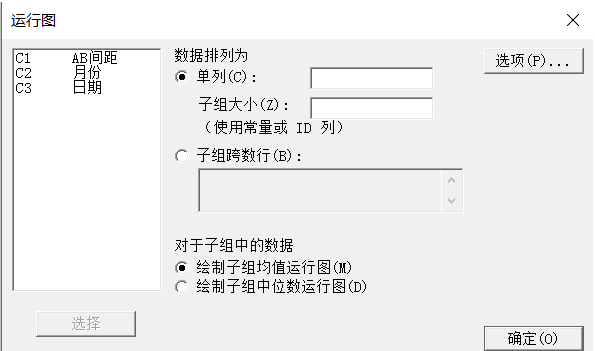
1. 统计 → 质量工具 → 运行图

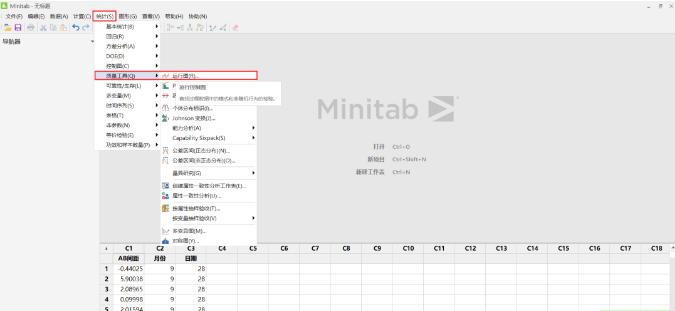
2. 单列内输入变量，根据所求输入子组大小（某点测量次数）

二、柏拉图

        柏拉图又称Pareto 图、主次因素图、排列图，其根据 Vilfredo Pareto 命名，原理为 80/ 20 原则，即 20% 的人拥有 80% 的财富，形式为按降序排列并带有累计百分比的曲线的特殊条形图。作为基本的质量控制工具之一，用来突出显示最常出现的缺陷或缺陷最常见的原因。条形要从大到小依次排列，其长短表示各组绝对数的大小，线段的上升表示累计百分比的增加情况，可直观找出主要因素和真正重要问题。将找出的主要因素和真正重要的问题作为改进质量目标；通过采取改进措施，可比较改进前后的柏拉图用以确定原来的主要因素是否存在或降为次要位置。

（一）汇总数据的柏拉图

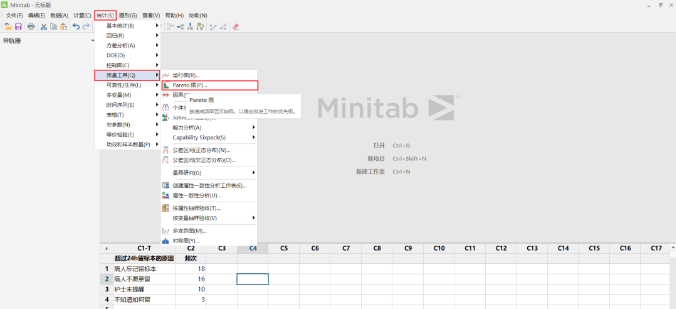
1. 统计 —— 质量工具 —— Pareto 图

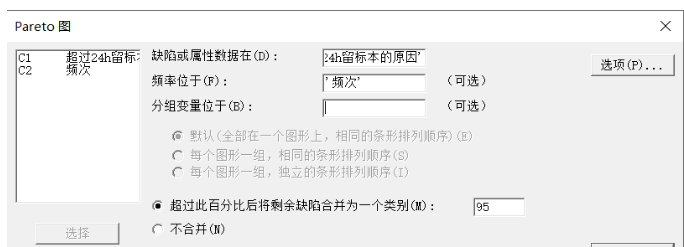
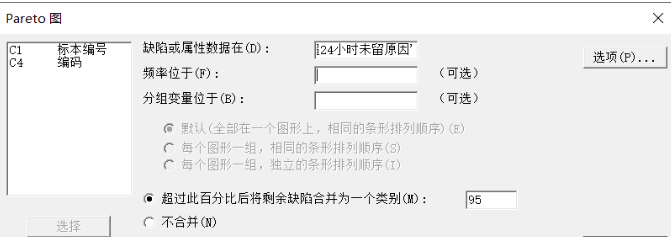
2. 在 Pareto 图中，【缺陷或属性数据在】输入缺陷或属性分类的变量，【频率位于】为包含缺陷或属性的汇总数据的变量；超过此百分比后将剩余缺陷合并为一个类别即默认将累计百分比超过95%的分组合并为一类，即“其他”。

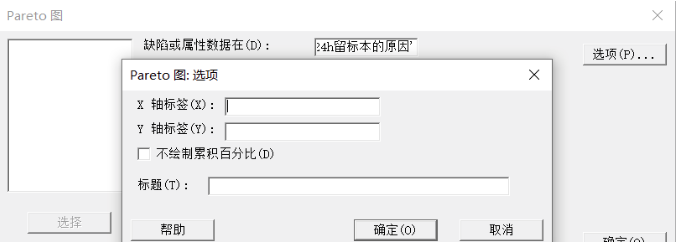
3.  选项主要用于设定 X 轴标签 、Y 轴标签及标题。

4. 主要结果及分析：排前 2 位的原因依次为病人忘记留标本和病人不愿意留，其累计百分比约为 80% ，为主要因素。

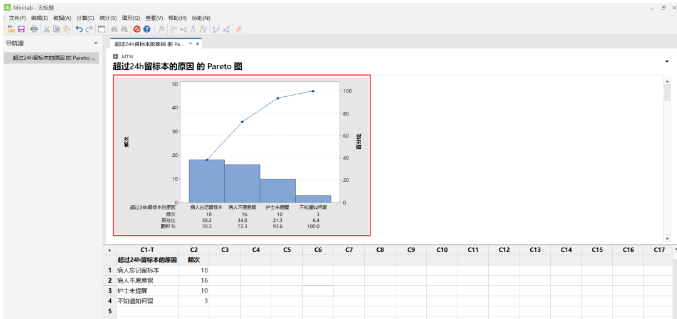
（二）原始数据的柏拉图

如使用原始数据的柏拉图，需要在数据右边添加属性及编码，【缺陷或属性数据】选择原始数据所在列，其余操作均相同。

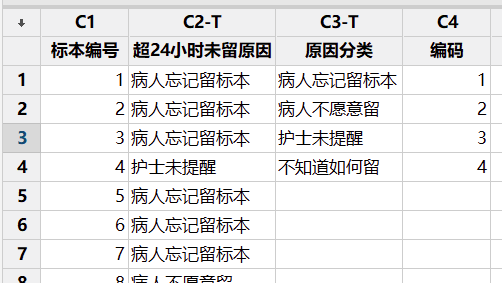
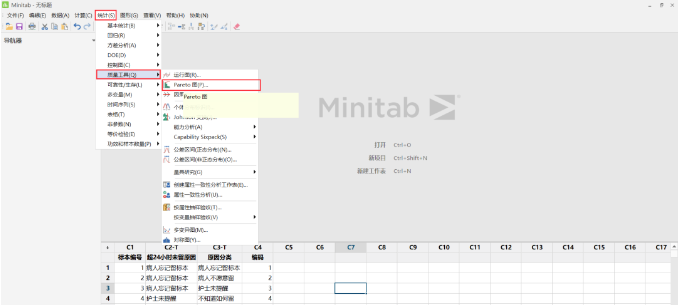
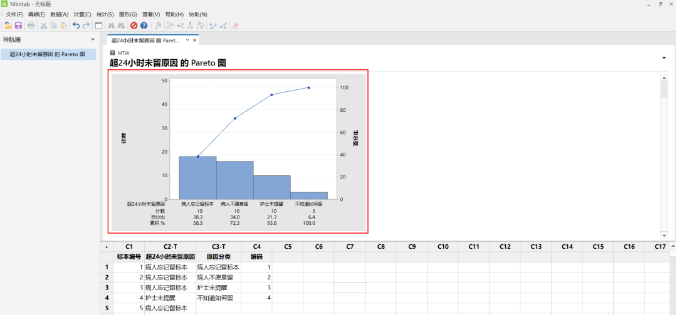
Minitab 所作柏拉图可能与主流Excel 所作柏拉图有所不同，例如折线图未从原点出发或者第一个点未通过柱形图的右上角等现在柏拉图的要求，但门槛低，使用起来非常方便，且并不影响寻找主要因素和真正重要问题。

上一条：fiddler软件是神器

下一条：Minitab常用图表，都总结在这了