Gurobi-第五章Gurobi线性化技巧

现在的最优算法规划求解软件都是基于线性规划原理而设计开发的,然而实际问题却千变万化它们的约束、目标等各不相同。如何对实际问题进行建模,并将它归结为一个线性规划问题,是应用线性规划求解问题时最重要,也是最困难的一步。问题建模是否合理,很大程度上会影响后续的模型求解过程。但是,由于受限于实际问题特征、建模经验、建模技巧等因素,在对问题建立初步模型之后,目标函数和约束条件往往会包含一此特殊约束或特殊变量,如绝对值、在集合中取最大值和最小值、二选一的问题等。尽管它们看起来不是线性规划问题,但是通过一些建模技巧,可以将其转化成线性规划问题,将非线性约束转换成线性约束为广义约束。  

广义约束不同于线性约束或函数约束，函数约束可以看成是连续光滑的函数表达式,如x+y+z>0,而广义约束更像是一种集合操作，分段函数,如h=max(x,y,z)，函数约束给人的感觉是可微函数空间,而广义约束是不可微的。虽然这么说不很恰当,但是广义约束的处理和平常接触到的优化模型的分析思路有很大的区别。接下来学习Gurobi中几个常见的广义约束表达式:max,minabs、and、or、indicator,range,sos等。  

添加广义约束有两种方法:一种是model类的方法add_XXX;另一种是model.addConstr方法。约束条件用Gurobi内置函数表示,即用gurobipy.XXX函数来表达广义约束。从可读性的角度来说推荐使用第二种方法。  

注意;当使用第二种方法时,该约束做的是逻辑判断,而不是赋值操作,这样就和model.addCon-str方法的输入要求一致了。  

一、最大值max  

max函数用来获取集合中的最大值,如z=max(x,y,3),这类问题可以通过大M法转成线性约束,即:  

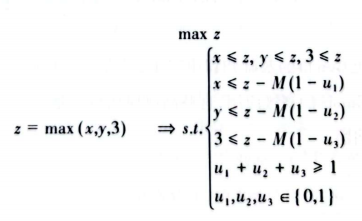
这里我们用到了大M法,大M法是数学规划中的一个建模技巧,通过引人一个极大的数M,结合约束条件,来实现逻辑运算功能。在本小节中,非线性问题线性化的一个重要方法就是通过大M法来实现。  

虽然线性化方法原理比较麻烦,但使用Gurobi接口是很容易实现这个功能的,下面演示常规的线性化方法和Gurobi内置的max_广义线性化接口的方法,其得到的结果是一样的,如代码所示。  

#方法1：使用转换后的约束  

#假设x=4,y=5  

importgurobipyasgrb  

#创建模型，定义变量  

m=grb.Model()  

x=m.addVar(name='x')  

y=m.addVar(name='y')  

z=m.addVar(name='z')  

u1=m.addVar(vtype='B',name='u1')  

u2=m.addVar(vtype='B',name='u2')  

u3=m.addVar(vtype='B',name='u3')  

M=10000  

#添加约束  

m.addConstr(x<=z-M*(1-u1),name='c1')  

m.addConstr(y<=z-M*(1-u2),name='c2')  

m.addConstr(3<=z-M*(1-u3),name='c3')  

m.addConstr(x==4,name='c4')  

m.addConstr(y==5,name='c5')  

m.addConstr(u1+u2+u3>=1,name='c6')  

m.addConstr(x<=z,name='c7')  

m.addConstr(y<=z,name='c8')  

m.addConstr(3<=z,name='c8')  

#定义目标函数并求解  

m.setObjective(z)  

m.optimize()  

print("z=",z.X)  

#输出  

#z=5  

下面演示使用Gurobi内置接口的方法,如代码所示  

#方法2：使用gurobi内置方法  

importgurobipyasgrb  

m=grb.Model()  

x=m.addVar(name='x')  

y=m.addVar(name='y')  

z=m.addVar(name='z')  

m.addConstr(x==4,name='c4')  

m.addConstr(y==5,name='c5')  

m.addConstr(z==grb.max_(x,y,3))  

m.setObjective(z)  

m.optimize()  

print("最大值是：z=",z.X)  

#输出z=5.0  

二、最小值min  

与max函数相对应的是min函数,获取集合中的最小值,以z=min(x,y,3)为例,使用大M法得到其对应的线性约束表达式,即:  

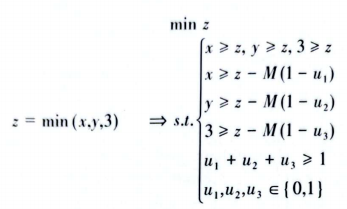
有了数学表达式,根据表达式写出相应的代码就很简单了,如代码所示。  

#方法1：使用转换后的约束  

importgurobipyasgrb  

m=grb.Model()  

x=m.addVar(name='x')  

y=m.addVar(name='y')  

z=m.addVar(name='z')  

u1=m.addVar(vtype='B',name='u1')  

u2=m.addVar(vtype='B',name='u2')  

u3=m.addVar(vtype='B',name='u3')  

M=10000  

m.addConstr(x>=z-M*(1-u1),name='c1')  

m.addConstr(y>=z-M*(1-u2),name='c2')  

m.addConstr(3>=z-M*(1-u3),name='c3')  

m.addConstr(x==4,name='c4')  

m.addConstr(y==5,name='c5')  

m.addConstr(u1+u2+u3>=1,name='c6')  

m.addConstr(x>=z,name='c7')  

m.addConstr(y>=z,name='c8')  

m.addConstr(3>=z,name='c8')  

m.setObjective(-z)  

m.optimize()  

print("z=",z.X)  

#输出z=3  

同理,可以写出Gurobi内置接口的方法,如代码所示  

#方法2：使用Gurobi的接口  

importgurobipyasgrb  

m=grb.Model()  

x=m.addVar(name='x')  

y=m.addVar(name='y')  

z=m.addVar(name='z')  

m.addConstr(x==4,name='c4')  

m.addConstr(y==5,name='c5')  

m.addConstr(z==grb.min_(x,y,3))  

m.setObjective(z)  

m.optimize()  

print("最小值是：z=",z.X)  

#输出z=3.0  

三、绝对值abs  

abs约束表示获取变量的绝对值,例如,有如下规划问题：  

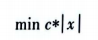
可令y=|x|,即y>=x,y>=-x,将原问题转换成如下新的问题：  

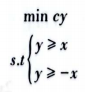
演示结果如代码所示。  

importgurobipyasgrb  

m=grb.Model()  

x=m.addVar(lb=-10,name='x')  

y=m.addVar(name='y')  

m.addConstr(y==grb.abs_(x),name='C_abs')  

m.addConstr(x>=-5,name='C_2')  

m.addConstr(x<=3,name='C_3')  

m.setObjective(y,-1)#求最大  

m.optimize()  

print("y=",y.X)  

print("x=",x.X)  

#输出  

#y=5.0  

#x=-5.0  

四逻辑与and  

如果集合中全部变量都是1,则结果为1,否则为0。判断集合中的变量是否全为1的实现功能类似Pandas中的any功能。例如,如果x=1且y=1,则z=1,否则z=0可以使用大M法结合0-1变量(0-1变量指的是取值只能是0或1的变量,又称二值变量)实现线性化,具体如下。  

令j=x+y-m+B,若j>0则z=1,否则z=0。其中变量的个数,此处m=2,B是一个很小的正数，因此将问题转换成指示函数indicator的线性化问题。  

五、逻辑或or  

集合中全部变量只要有一个是1则结果为1,否则为0,即实现“不全为0”的判断,如有下面的问题:  

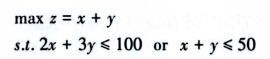
可使用大M法转成线性规划,具体如下:  

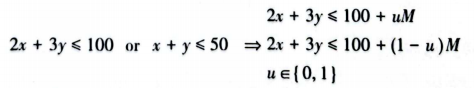
六、指示函数indicator  

如果指示变量的值为1,则约束成立,否则约束可以被违反。例如,如果x>0,则y=1,否则y=0,indicator的线性化方法可以使用大M法实现,原理如下;  

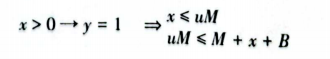
式中,M是一个很大的数,B是一个很小的正数。  

在Gunbi中实现该功能的是函数addGenConstrIndicator,使用方法如代码所示  

importgurobipyasgrb  

model=grb.Model()  

x=model.addVar(name='x')  

y=model.addVar(name='y')  

model.addConstr((y==1)>>(x>0),name='indicator')  

七、带固定成本约束  

在库存问题中,通常会考虑订货的固定成本和可变成本。就是说,只要订货x>0就有一个固定成本k和可变成本cx,它的成本函数是:  

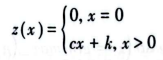
这实际上是一个二选一约束,使用大M法即可转成线性约束,即:  

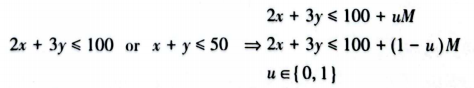
八、分段线性函数  

在现实生活中,购买商品的数量越多就会有折扣,其单价就越低。在数学中,它的成本或利润函数可以表示为如下的分段线性函数:  

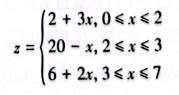
对于分段线性函数,可以通过引入SOS2约束(aSpecialOrderSetConstraintofType2),将其转换为线性规划。  

然而还有一个更通用的方法,设有一个n段线性函数f(x)的分界点  

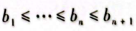
,引入wk将x和f(x)表示为:  

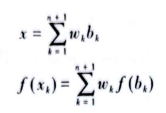
wk和zk满足以下约束:  

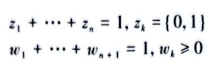
前面已经讲了许多非线性模型线性化的方法,需要注意的是,在使用Gurobi的广义线性化函数时,不能对表达式做线性化,而需要先将表达式赋予变量,然后再对变量做线性化,例如:  

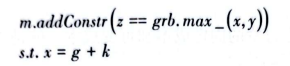
是正确的,而  

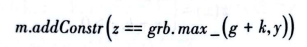
则是错误的。

上一条：Gurobi-第四章Gurobi属性和修改方法

下一条：Gurobi-第六章Gurobi多目标优化