Gurobi-第六章Gurobi多目标优化

一、概述  

多目标优化就是同时求解多个目标。多目标其实也很好理解,可以理解为在工作时要保证工作质量的前提下压缩时间以加快进度,这里面就有两个目标:一个是保证工作质量;另一个是压缩时间加快进度。在多目标优化中,可以直接把多个目标通过分配权重的方式组合成单目标优化问题,但是如果多个目标函数之间的数量级差异很大,则应该使用分层优化的方法。  

二、Gurobi多目标优化模型  

在Gurobi中,可以通过Model.setObjectiveN函数来建立多目标优化模型,多目标的setObjectiveN函数和单目标的setObjetive函数用法基本一致,不同的是多了目标优先级、目标劣化接受程度、多目标的权重等参数。

  

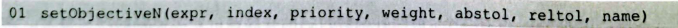
各参数说明如下  

(1)expr;目标函数表达式,如x+2y+3z。  

(2)index:目标函数对应的序号(0,1,2,··),即第几个目标,注意目标函数序号应从0开始。  

(3)priority:优先级，为整数，值越大表示目标优先级越高。  

(4)weight:权重（浮点数），在合成型多目标解法中使用该参数，表示不同目标之间的组合权重。  

(5)abstol:允许的目标函数最大降低量，即当迭代的值相比最优值的可接受的劣化程度。  

(6)reltol：abstol的百分比表示，0.05表示可接受的劣化程度是5%  

(7)name：目标函数名称  

需要注意的是,在Gurobi的多目标优化中,要求所有的目标函数都是线性的,并且目标函数的优化方向一致、即全部最大化或全部最小化,因此可以通过乘以-1实现不同的优化方向，  

当前Gurobi支持3种多目标模式,分别是Blend(合成型),Hherarrhieal(分层型),两者的混合型。多目标的详细解法将在后续重节讲解。  

Blend通过对多个目际赋予不同的权重实现将多目标转化成单目标函数，权重扮演优先级的角色。  

下面演示Gurobi多目标优化的使用方法。  

#合成型  

importgurobipyasgrb  

model=grb.Model()  

x=model.addVar(name='x')  

y=model.addVar(name='y')  

#添加第1个目标  

model.setObjectiveN(x+2*y,index=0,weight=3,name='obj1')  

#添加第2个目标  

model.setObjectiveN(x-3*y,index=1,weight=0.5,name='obj2')  

Hierarchical有优先级，一般理解是在保证第一个目标值最优的情况下代化第二个目标,或者在优化第二个目标时要保证第一个目标的最优值只能允许少量劣化,例如,有如下两个优化目标。  

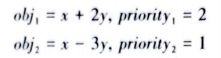
此时Gurobi按照优先级大小进行优化(先优化objl,再优化obj2)。若没有设定abstol或reltol,则在优化低优先级目标(obi2)时,不会改变高优先级的目标(obi1)值,如代码所示。  

#分成型  

importgurobipyasgrb  

model=grb.Model()  

x=model.addVar(name='x')  

y=model.addVar(name='y')  

#添加第1个目标  

model.setObjectiveN(x+2*y,index=0,priority=20,name='obj1')  

#添加第2个目标  

model.setObjectiveN(x-3*y,index=1,priority=1,name='obj2')  

混合型的写法也很简单,将权重和优先级同时设定即可,如代码所示。  

#混合型  

importgurobipyasgrb  

model=grb.Model()  

x=model.addVar(name='x')  

y=model.addVar(name='y')  

#添加第1个目标  

model.setObjectiveN(x+2*y,index=0,weight=3,priority=20,name='obj1')  

#添加第2个目标  

model.setObjectiveN(x-3*y,index=1,weight=0.5,priority=1,name='obj2')  

前面讲了如何设定优先级,接下来看看如何获取各个目标的优化值,演示代码如下。  

#获取目标函数值  

foriinrange(2):  

m.setParam(grb.GRB.Param.ObjNumber,i)  

print('Obj%d='%(i+1),m.ObjNVal)  

三、Gurobi多目标优化示例  

通过一个简单的例子来说明Gurobi的多目标优化问题。假设工厂需要把N份工作分配给N个工人,每份工作只能由一个工人做,且每个工人也只能做一份工作,假设工人i处理工作j需要的时间是T;,获得的利润是C,那么需要怎么安排才能使得总利润最大且总耗时最小呢?这里有两个目标,最主要的目标是利润最大化,次要目标是耗时最小化,下面来看看Gurobi是怎么求解这个问题的。  

为了编程方便,这里假设N=10,Tij和Cij通过随机数生成,演示结果如代码所示。  

importgurobipyasgrb  

importnumpyasnp  

#设定工人数和工作数量  

N=10  

np.random.seed(1234)#固定随机数种子，这样每次产生的随机数一样  

#用随机数初始化时间矩阵Tij和成本矩阵Cij  

#i+1,j+1是为了序号从1开始编号  

Tij={(i+1,j+1):np.random.randint(0,100)foriinrange(N)forjinrange(N)}  

Cij={(i+1,j+1):np.random.randint(0,100)foriinrange(N)forjinrange(N)}  

#定义model  

m=grb.Model('MultiObj')  

#添加变量，x是tupledict类型，可以方便使用select,sum,prod函数  

#同时可以加快创建变量的效率  

#x是0-1类型变量，xij=1表示第i个工人被分配到第j个工作中  

x=m.addVars(Tij.keys(),vtype=grb.GRB.BINARY,name='x')  

#添加约束  

#tupledict的sum函数使用  

#第一个约束表示一个工作只能分配给一个工人  

#第二个约束表示一个工人只做一个工作  

m.addConstrs((x.sum('*',j+1)==1forjinrange(N)),'C1')  

m.addConstrs((x.sum(i+1,'*')==1foriinrange(N)),'C2')  

#多目标方式1：Blend合成型  

#设置多目标权重  

#x.prod(Tij)表示工人分配矩阵Xij和时间矩阵Tij通过相同的索引ij进行相乘  

#这也是Gurobi扩展tupledict的原因  

#第二个目标函数取符号是为了保证两个目标的优化方向一致  

#m.setObjectiveN(x.prod(Tij),index=0,weight=0.1,name='obj1')  

#m.setObjectiveN(-x.prod(Cij),index=1,weight=0.5,name='obj2')  

#多目标方式2：Hierarchical分层型  

m.setObjectiveN(x.prod(Tij),index=0,priority=1,abstol=0,reltol=0,name='obj1')  

m.setObjectiveN(-x.prod(Cij),index=1,priority=2,abstol=100,reltol=0,name='obj2')  

#启动求解  

m.optimize()  

#获得求解结果  

#x[i].x表示获取某个变量的值  

foriinTij.keys():  

ifx[i].x>0.9:  

print("工人%d分配工作%d"%(i[0],i[1]))  

#获取目标函数值  

foriinrange(2):  

m.setParam(grb.GRB.Param.ObjNumber,i)  

print('Obj%d='%(i+1),m.ObjNVal)  

#输出结果  

#Obj1=373.0  

#Obj2=-768.0  

#工人1分配工作8  

#工人2分配工作10  

#工人3分配工作9  

#工人4分配工作3  

#工人5分配工作2  

#工人6分配工作4  

#工人7分配工作5  

#工人8分配工作7  

#工人9分配工作1  

#工人10分配工作6  

上面的代码是一个简单的整数规划模型,首先定义了每个工人和人物的时间矩阵和成本矩阵，然后定义模型,并添加约束,即每个工人只能做一份工作,一份工作也只能由一个工人完成，然后使用分层多目标规划的方法来设置目标函数,最后求解。可以看到,通过Gurobi的多目标规划接口可以很快求解完成多目标优化建模问题。  

上一条：Gurobi-第五章Gurobi线性化技巧

下一条：Gurobi-第七章Gurobi callback函数