- 标签
- 热门文章
- 推荐文章
gurobi的安装、基础使用及学习资料
Gurobi是一个用于数学优化的高性能求解器,广泛应用于供应链管理、资源分配、生产调度等领域。
它提供了Python接口,使得使用Python语言能够方便地构建和求解优化模型。本文介绍Python中Gurobi的用法及案例。
安装和导入
首先需安装Gurobi并导入相关的Python模块。可在Gurobi官方网站上下载和安装适用于你的操作系统的版本。
也可直接pip安装,直接安装的版本为免费版,变量数量有限制,若要学术版本或者商业版本需要去官网申请license。
pip install gurobipy
安装完成后,可以在Python环境中导入使用。
import gurobipy
模型构建
要使用Gurobi求解优化问题,首先需要构建一个模型。
Model()
函数创建一个新模型对象。
addVar()
添加变量。
addConstr()
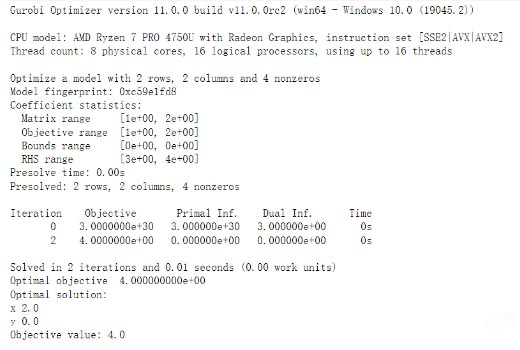
下面是一个简单的线性规划示例,求解最大化目标函数2x + y的问题:
import gurobipy as grb
# 创建模型对象
model = grb.Model()
# 添加变量
x = model.addVar(vtype=grb.GRB.CONTINUOUS, lb=0, name="x")
y = model.addVar(vtype=grb.GRB.CONTINUOUS, lb=0, name="y")
# 添加约束条件
model.addConstr(x + 2*y <= 3, "c0")
model.addConstr(2*x + y <= 4, "c1")
# 设置目标函数
model.setObjective(2*x + y, grb.GRB.MAXIMIZE)
# 模型求解
model.optimize()
# 输出结果
print("Optimal solution:")
for var in model.getVars():
print(var.varName, var.x)
print("Objective value:", model.objVal)
数据处理
在实际应用中,我们经常需要从外部文件或数据库中读取数据,并将其应用于模型中。Gurobi提供了方便的接口来处理数据。
# 从文件中读取数据
model.read("data.lp")
使用setAttr()方法设置变量的属性。
# 设置变量的属性
model.setAttr("ub", x, 5)
基础案例
接下来,我们将通过一个实际案例来演示Gurobi的用法。假设我们有一家工厂需要生产两种产品,分别为A和B,需要决定生产数量以最大化利润。每种产品的生产时间和材料成本如下:

工厂每天有8个小时的生产时间和50元的成本限制。我们的目标是最大化利润。下面是求解该问题的代码示例:
import gurobipy as grb
# 创建模型对象
model = grb.Model()
# 添加变量
x = model.addVar(vtype=grb.GRB.INTEGER, lb=0, name="x")
y = model.addVar(vtype=grb.GRB.INTEGER, lb=0, name="y")
# 添加约束条件
model.addConstr(4*x + 3*y <= 8, "c0")
model.addConstr(6*x + 8*y <= 50, "c1")
# 设置目标函数
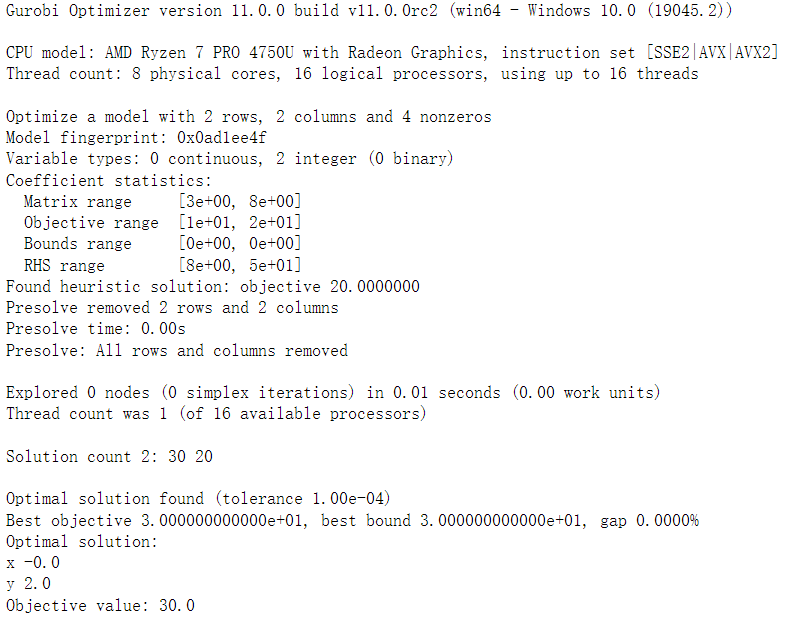
model.setObjective(10*x + 15*y, grb.GRB.MAXIMIZE)
# 模型求解
model.optimize()
# 输出结果
print("Optimal solution:")
for var in model.getVars():
print(var.varName, var.x)
print("Objective value:", model.objVal)
数据处理
在实际应用中,我们经常需要从外部文件或数据库中读取数据,并将其应用于模型中。Gurobi提供了方便的接口来处理数据。
# 从文件中读取数据
model.read("data.lp")
使用setAttr()方法设置变量的属性。
# 设置变量的属性
model.setAttr("ub", x, 5)
基础案例
接下来,我们将通过一个实际案例来演示Gurobi的用法。假设我们有一家工厂需要生产两种产品,分别为A和B,需要决定生产数量以最大化利润。每种产品的生产时间和材料成本如下:
工厂每天有8个小时的生产时间和50元的成本限制。我们的目标是最大化利润。下面是求解该问题的代码示例:
import gurobipy as grb
# 创建模型对象
model = grb.Model()
# 添加变量
x = model.addVar(vtype=grb.GRB.INTEGER, lb=0, name="x")
y = model.addVar(vtype=grb.GRB.INTEGER, lb=0, name="y")
# 添加约束条件
model.addConstr(4*x + 3*y <= 8, "c0")
model.addConstr(6*x + 8*y <= 50, "c1")
# 设置目标函数
model.setObjective(10*x + 15*y, grb.GRB.MAXIMIZE)
# 模型求解
model.optimize()
# 输出结果
print("Optimal solution:")
for var in model.getVars():
print(var.varName, var.x)
print("Objective value:", model.objVal)
经典案例TSP问题
旅行商问题(Traveling Salesman Problem,简称TSP)是一个经典的组合优化问题,即寻找一条路径,使得从一个城市出发,恰好经过所有其他城市一次后回到起始城市,并使得总路程最短。
Gurobi可以用于求解TSP问题的近似解。下面是一个示例:
import gurobipy as grb
# 读取城市之间的距离矩阵
distances = [
[0, 2, 9, 10],
[1, 0, 6, 4],
[15, 7, 0, 8],
[6, 3, 12, 0]
]
n = len(distances) # 城市数量
# 创建模型对象
model = grb.Model()
# 添加二进制变量表示是否经过某个城市
x = {}
for i in range(n):
for j in range(n):
if i != j:
x[i, j] = model.addVar(vtype=grb.GRB.BINARY, name=f"x_{i}_{j}")
model.update()
# 添加约束条件1:每个城市只能经过一次
for i in range(n):
model.addConstr(grb.quicksum(x[i, j] for j in range(n) if j != i) == 1)
# 添加约束条件2:从一个城市出发,只能到达一个城市
for j in range(n):
model.addConstr(grb.quicksum(x[i, j] for i in range(n) if i != j) == 1)
# 添加目标函数:最小化总路程
model.setObjective(grb.quicksum(distances[i][j] * x[i, j] for i in range(n) for j in range(n) if i != j), grb.GRB.MINIMIZE)
# 模型求解
model.optimize()
# 输出结果
if model.status == grb.GRB.OPTIMAL:
print("Optimal solution found!")
for i in range(n):
for j in range(n):
if i != j and x[i, j].x > 0.5:
print(f"City {i} -> City {j}")
print(f"Total distance: {model.objVal}")
else:
print("No solution found.")
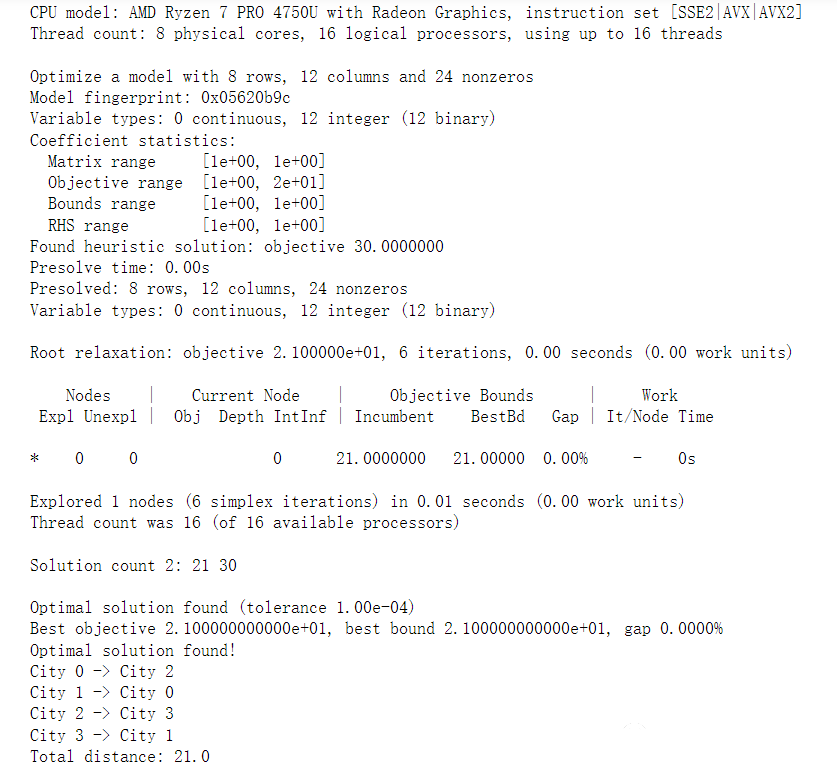
最优线路为:city0-city2-city3-city1-city0
总距离为:21
在这个示例中,我们首先定义了城市之间的距离矩阵。
然后,创建了一个二进制变量x来表示是否经过每个城市。
接着,添加了约束条件1和约束条件2,分别保证每个城市只经过一次,并且从一个城市只能到达一个城市。
最后,设置了目标函数为最小化总路程。
通过调用model.optimize()方法,Gurobi将尝试找到总路程最短的路径。如果找到了最优解,则输出每个相邻城市之间的路径和总路程。如果没有找到最优解,则输出"No solution found."。
TSP是一个NP-hard问题,对于大规模的问题,完全求解的时间复杂度是指数级别的。在实际应用中,可能需要使用其他启发式算法来求解。可参考我之前的文章。
总结
本文介绍了Python中Gurobi的基础用法。Gurobi提供了强大而灵活的数学优化求解能力,可以帮助我们求解各种复杂的优化问题。
通过使用Gurobi我们可以更加高效地解决实际问题。希望本文对大家应用Gurobi有所帮助。
上一条:Postman中参数填写方式



