Python + Gurobi 求解运输问题入门

运输问题介绍

  一般的运输问题就是要解决以下问题：把某种产品从若干个产地调运到若干个销地，在每个产地的供应量与每个销地的需求量已知，并知道各地之间的运输单价的前提下，如何确定一个使得总的运输费用最小的方案。

符号设定

A1，A2，……Am表示某种产品的m个产地；

B1，B2，……Bn表示某种产品的n个销地；

si表示产地Ai的产量；

dj表示销地Bj的销量。

cij表示把产品从产地Ai运到销地Bj的单位运价；

数学模型

设xij表示从产地Ai运到销地Bj的产品运输量，则数学模型如下：

目标函数：

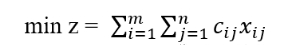
约束条件：

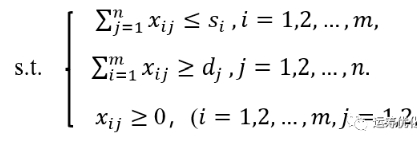
例子

  喜庆食品公司有三个生产面包的分厂A1，A2，A3，有四个销售公司B1，B2，B3，B4，各厂产量（吨）、销量（吨）及单位运价（百元/吨）如表所示：

B1B2B3B4产量

A13113107

A219284

A3741059

销量/t365620

数学模型

例子数学模型如下：

目标函数：

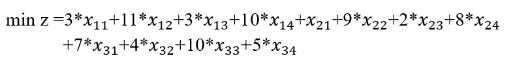
约束条件：

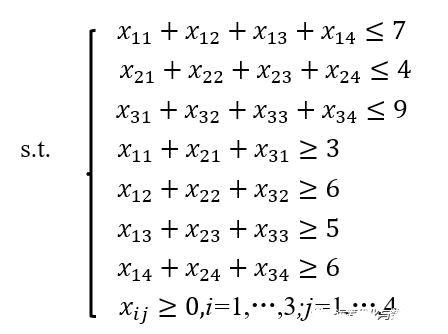
调用gurobi求解

#数据准备

 supplyNum=3           #供应商数量

 demandNum=4           #需求商数量

 A=np.array([7,4,9])           #产量

 B=np.array([3,6,5,6])         #销量

 C=np.array([[3,11,3,10],[1,9,2,8],[7,4,10,5]])  #成本

 supply=[i for i in range(supplyNum)]    #供应商点集合

 demand=[i for i in range(demandNum)]    #零售商点集合

 

 #构建模型

 model=Model('transportation')

 x={}      #创造一个决策变量的储存列表

  

 #添加决策变量

 for i in supply:

     for j in demand:

         name='x'+str(i)+'_'+str(j)

         x[i,j]=model.addVar(0,GRB.INFINITY,vtype=GRB.CONTINUOUS,name=name)

 #添加目标函数

 model.setObjective(sum(x[i,j]*C[i,j] for i in supply for j in demand),GRB.MINIMIZE)

 #添加产量约束

 for i in supply:

     model.addConstr(sum(x[i,j] for j in demand)<=A[i])

 #添加销量约束

 for j in demand:

     model.addConstr(sum(x[i,j] for i in supply)>=B[j])

 # 模型求解

 model.optimize()

  

 #结果输出

 for key in x.keys():

     if x[key].x>0:

         print(x[key].Varname,x[key].x)

 print('最小成本为：',model.ObjVal) 

解信息

B1B2B3B4

A12050

A21003

A30603

最小运输成本为8500元

画图

# 运输问题的结果

 result = np.array([[2, 0, 5, 0],

                    [1, 0, 0, 3],

                    [0, 6, 0, 3]])

 

 # 绘制柱状图

 fig, ax = plt.subplots()

 ax.bar(np.arange(4), result[0], label='Factory 1')

 ax.bar(np.arange(4), result[1], bottom=result[0], label='Factory 2')

 ax.bar(np.arange(4), result[2], bottom=result[0]+result[1], label='Factory 3')

 

 # 设置图形属性

 ax.set_xticks(np.arange(4))

 ax.set_xticklabels(['Company 1', 'Company 2', 'Company 3', 'Company 4'])

 ax.set_ylabel('Quantity')

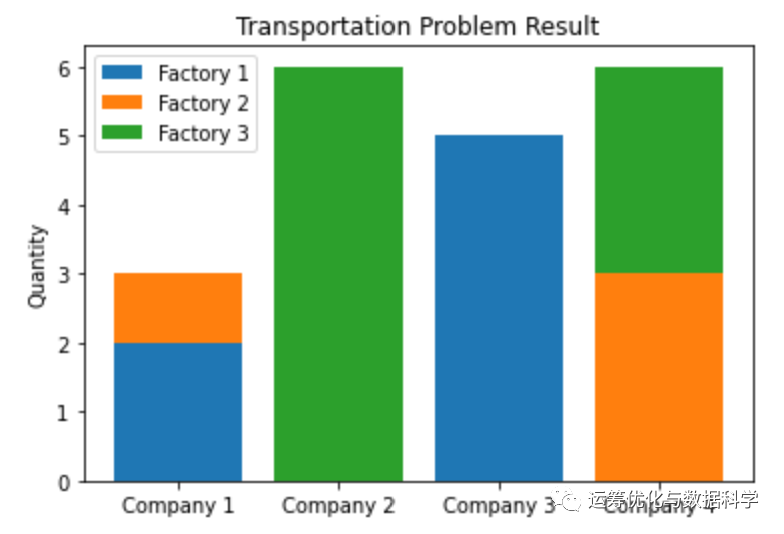
 ax.set_title('Transportation Problem Result')

 ax.legend()

 

 # 显示图形

 plt.show()

上一条：gurobi的安装、基础使用及学习资料

下一条：在服务器上搭建gurobi环境