Gurobi求解数独问题

本文以Gurobi官方提供的数独案例为例，将介绍以下知识点：

设置变量的属性Attribute

如何固定变量的值

使用生成器添加多个约束

quicksum() 函数的使用

设置变量的属性

Gurobi中的Var类具有多个属性(Attribute)，如LB，UB，Obj等。

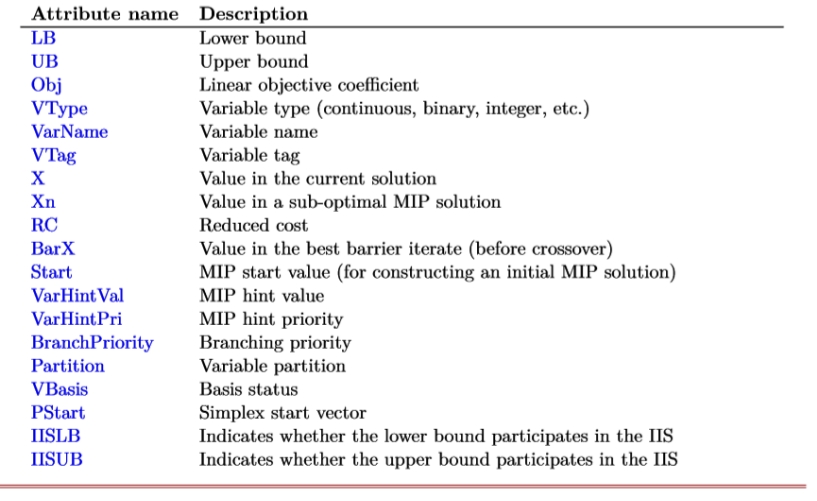
这些属性可以在创建变量时，使用关键字参数传入，也可以调用相应的方法进行相应的更改

# 创建一个目标汉中的系数为2.0，变量名称为x的0-1变量

x = m.addVar(obj = 2.0, vtype = GRB.BINARY, name = 'x')

# 在得到Var对象后，再对属性进行修改

var.setAttr(GRB.Attr.UB, 0.0)

var.setAttr("ub", 0.0)

# 可以直接用.访问其属性

var.UB = 0

固定变量的值

如果要固定某一变量的值，可以令该变量的上限和下限等于同一个常数

constant = 9

var.UB = constant

var.LB = constant

注意固定变量的值不等同于变量中Start属性。Start属性为MIP问题中的初始解，可以用一些启发式规则得到该问题的某一可行解，并以此进行计算。之后的初始解可能会发生改变。因此，应注意区分。

生成器生成多个约束

生成器生成多个约束

Python中的生成器(generator)对象，可以在需要的时候再对某一循环进行按需调用。详情可通过廖雪峰老师的教程了解。

在Gurobi中，生成器通常按照列生成式的方法编写，只不过将外部的方括号[]变为圆括号()

# 生成一个2*x列表 （x= 1,...,9)

>>> L = [2x for x in range(10)]

>>> L

[0, 2, 4, 6, 8, 10, 12, 14, 16, 18]

>>> g = (2x for x in range(10))

>>> g

<generator object <genexpr> at 0x1022ef630>

在日常建模中，通常针对某一集合中的每个元素遍历并添加约束，如：

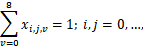
我们可以使用m.addConstr()，针对每一种i,j的组合，为其添加约束。

Gurobi也支持将生成器传入m.addConstrs()， 以达到批量添加的目的。

# 创建3维0-1变量

vars = m.addVars(n, n, n, vtype=GRB.BINARY, name="G")

for i in range(n):

    for j in range(n):

        m.addConstr(vars.sum(i,j,'*')==1)

# 等价于

m.addConstrs((

      vars.sum(i,j,'*')==1 

      for i in range(n) 

      for j in range(n)))

两种写法的区别仅仅是将for循环写在外面还是使用生成器，其他方面没有区别，但前者的可读性可能会稍强些

quicksum()函数的使用

quicksum(data)是Gurobi推荐的求和函数，其执行效率高于Python内置的sum()函数。因此，在大规模添加模型时，建议优先使用quicksum()

quicksum(data)接受含有Var或者表达式(LinExpr, QuadExpr)的List对象，并将其中的所有的元素相加，生成求和表达式

expr = quicksum([2*x, 2*y+1, 4*z*z])

expr = quicksum([x, y, z])

上文中的案例，除了可以用tupledict的sum函数，也可以写作quicksum。

不过tupledict的sum方法支持通配符*，书写起来更加简便。

for i in range(n):

    for j in range(n):

    # 对于当前的i和j，在v维度上进行求和

        m.addConstr((gp.quicksum(vars[i,j,v] for v in range(n))==1)

前面说data需要List类型的对象，此处可以理解为生成器作为参数传入list()函数中，可以一次性将生成器转化为list对象

数独案例

参考自Gurobi自带的案例文件根目录/examples/python/sudoku.py

如果要运行该案例，需要在命令行中添加数据文件根目录/examples/data/sudoku1

数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

本案例采用三维0-1决策变量x(i,j,v)，x(i,j,v)=1代表在第i行j列的格子上填的数字为v+1(i, j, k均从0开始计数)；否则，x(i,j,v)=0。

因此，具有以下约束：

以下是本人增加中文注释后的代码，希望通过前面的解读，还是比较易懂的。

import gurobipy as gp

from gurobipy import GRB

import math

"""

假设数独模型是这个样子

.284763..

...839.2.

7..512.8.

..179..4.

3........

..9...1..

.5..8....

..692...5

..2645..8

"""

# 假设数据存放在同目录下的data文件夹下

f = open("./data/sudoku1")

grid = f.read().split()

n = len(grid)

s = int(math.sqrt(n) )

m = gp.Model()

vars = m.addVars(n, n, n, vtype=GRB.BINARY,name="G")

#读入数据，将已知的

for i in range (n):

for j in range(n):

#如果该位置的数已知，则通过设置LB的方式，固定变量

if grid[i][j] !='.':

注意此处索引方式的不同

# grid为二维list，vars为dict

v= int(grid[i][])-1

vars[i,j,v].LB=1

#同一个位置，只能选一个数字

for i in range(n):

for j in range (n):

m.addConstr (vars.sum(i,j,'*')==1)

等价于

#m.addConstrs((

vars.sum(i,j,'*')==1

for i in range(n)

for j in range(n)))

添加行约束

#对于每行而言，每个数字只能出现一次

for i in range(n):

for v in range (n):

m.addConstr (vars.sum(i,'*',v)=1)

等价于

m.addConstrs((

vars.sum('*',j,v)==1

for i in range (n)

for v in range(n)))

# 添加列约束

#对于每列而言，每个数字只能出现一次

for j in range(n):

for v in range (n):

m.addConstr(vars.sum('*', j,v) ==1)

等价于

# m.addConstrs((

vars.sum(i,'*',v)==1

for j in range(n)

for v in range(n) ))

#

添加子矩阵约束

每个子矩阵内，数字不能重复

for i0 in range(3):

for jo in range(s):

for v in range(n):

m.addConstr (gp.quicksum(vars[i，j，v] for i in range(

10*s,(i0+1)*s) for j in range(j0*s, (j0+1)*s) ) == 1)

等价于

# m.addConstrs((

gp.quicksum(vars[i，j， v] for i in range(i0*s,(i0+1)*s) for j in range(j0*s，(j0+1)*3))-- 1

for i0 in range(s)

for j0 in range (s)

for v in range (n)))

开始优化模型

m.optimize()

获取vars变量的x属性

获得的tupledict对象，solution

solution = m.getAttr('X', vars)

for i in range(n):

sol ="'

for j in range(n):

for v in range (n) :

if solution[i,j，v] > 0.5:

301 += str (v+1)

print(s0l)

上一条：GUROBI数学规划优化器

下一条：化工流程模拟技术软件简介