GraphPad Prism 嵌套t检验和方差分析

　　嵌套因素概述

　　含两种处理的嵌套设计示例

　　实验设计

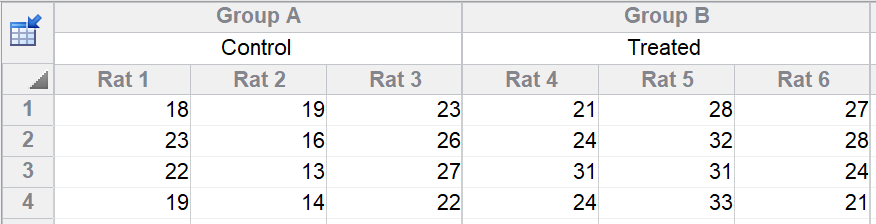
　　您在对照组和处理组大鼠中测量一个变量。每组有三只大鼠，且在每只大鼠中测量四个技术重复。注意：每个子列中堆叠的四个数值顺序是任意的，这四行的顺序不存在时间进程或其他特定含义。

        

　　为何是嵌套(设计)?

　　该设计被称为嵌套设计，原因是每只大鼠要么属于对照动物，要么属于处理动物。您无法探究某些大鼠对处理的反应是否优于其他大鼠，因为每只大鼠仅接受一种处理方式。此时，大鼠可认为是嵌套于“处理”因素之中。

　　这种设计也被称作分层设计。“Hierarchical(分层)”和“Nested(嵌套)”是描述此类设计的同义词。

　　错误分析：对全部数据进行t检验

　　将这些数据当作每组n=12(即每组12个样本)来处理，虽看似容易操作，但并不恰当。

         

　　若您对这些数据进行t检验，均值差异的95%置信区间为3.2至10.5，检验“来自均值相同总体的抽样”这一原假设的双侧P值为0.0008。这看似是“处理因素提升了结果变量”的有力证据，但这些结果实则无意义。

　　为何无意义？因为t检验假定每个数值提供独立信息。这些数据中，每种处理对应3只独立大鼠，但并非有12个独立测量值。换种说法：每只动物的重复测量值，相互间的相似度高于与其他动物测量值的相似度。当您合并3只重复的大鼠，以及每只大鼠内的4个技术重复时，得到的12个数值是伪重复值。将伪重复值当作真实重复值分析，会使置信区间过窄、P值过小。

　　错误分析：双因素方差分析

　　上方展示的数据，看似可用于双因素方差分析设置。但执行双因素方差分析会得出错误或误导性结果。双因素方差分析会假定“数据在第2行的大鼠，以某种方式同时接触对照和处理条件”。但实际每个子列中数值的顺序是任意的，因此在双因素方差分析中把“行”当作一个“因素”检验毫无意义。

　　无嵌套t检验的替代分析(仅在样本量相等时适用)

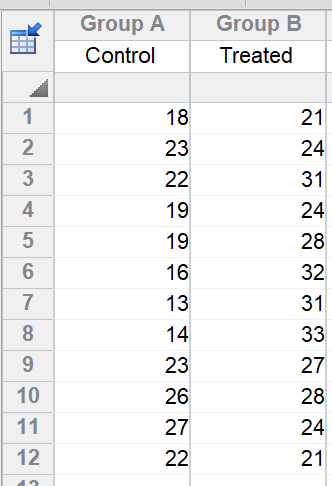
　　若不存在缺失值，您可用t检验分析数据。第一步是对每只大鼠的技术重复求均值。随后将这些均值录入新表格，再用非配对t检验(unpairedttest)比较两组均值。需注意：每组的三只大鼠，在t检验中是堆叠在一列，而在嵌套t检验中是子列并排呈现。

     

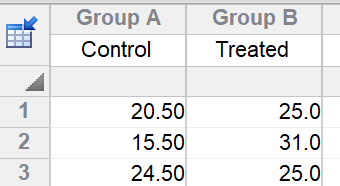
　　只要无缺失值，这种分析会给出正确结果。基于此正确结果，均值差的95%置信区间为-2.3至15.9，P值为0.1058。需注意：此处结论(无证据表明处理有效果)，与分析伪重复得出的错误结论大相径庭。

　　Prism中的嵌套t检验

　　Prism8开始引入了这项分析——嵌套t检验，可一步完成分析，且能够处理缺失值。其假定：子列均值是从“子列均值的高斯(正态)总体”中抽样获得，子列内的重复测量值是从一个高斯(正态)总体中抽样获得。通常，这两个高斯总体的标准差不同，Prism会计算(估计)二者，并以标准差和方差形式报告结果。

　　含三种处理的嵌套设计示例

　　实验设计

　　本示例源自优秀在线统计学文本《如何避免与识别统计滥用》。该研究评估两种病媒控制方法与无控制措施，对牛红细胞压积(PCV，packedcellvolume)的影响。选取3群牛，随机分配至3种处理组。从每群牛种抽取4头牛的血样，测定红细胞压积并制表。

　　我们关注的因素是“处理(treatment)”，嵌套因素是“牛群(herd)”。每群牛仅接受一种处理，因此“牛群”嵌套于“处理”种。

　　为何是嵌套设计？

　　该设计被称为嵌套(nested)，是因为每群牛要么作为对照组，要么接受一种处理。您无法探究“某些牛群对处理的反应是否优于其他牛群”，因为每群牛仅接受一种处理。牛群可说是嵌套于“处理”因素之中。

　　这种设计也叫分层设计(hierarchicaldesign)。

　　错误分析：对全部数据进行单因素方差分析

　　将这些数据当作“3个处理组中每组n=12”来处理，虽看似简单直接，但并不恰当。

　　若对这些数据进行单因素方差分析，结果无意义。方差分析假定每个数值提供独立信息。每种处理对应3群牛(每群牛采集4头牛的数据)，但并非每种处理有12个独立测量值。同一牛群内每头牛的重复测量值，相互间的相似度高于与其他牛群牛只测量值的相似度。

　　若如此分析数据，P值几乎肯定会过小，均值差的置信区间也会过窄。

　　错误分析：双因素方差分析

　　本节中上方的数据，看似可设置为双因素方差分析。但执行双因素方差分析会得出错误或误导性结果。双因素方差分析会假定“数据在第2行的所有牛只，以某种方式相互关联”，但实际并非如此。实际上，每个子列中数值的顺序是任意的，因此在双因素方差分析里将“牛只”作为一个“因素”检验毫无意义。

　　无嵌套方差分析的替代分析(仅在样本量相等时适用)

　　若无缺失值，您可用单因素方差分析分析数据。第一步是对每群牛的技术重复求均值。接着将这些均值录入新表格，再用单因素方差分析比较三组均值。

　　需注意：每种处理组的3群牛，在单因素方差分析中式堆叠在一列，而在嵌套t检验中是在子列并排呈现。

　　无缺失数据时，对这些均值数据进行单因素方差分析，与对整个数据集进行嵌套单因素方差分析结果一致。

　　术语：嵌套t检验与嵌套单因素方差分析

　　Prism使用一套独特的术语。

　　当存在两组数据集时，Prism提供嵌套t检验。我们选用该名称，是因为它最能描述此检验的用途：您想要比较两个处理组，同时存在另一个需考虑的嵌套变量，但这并非主要目的。该术语使用并不广泛，且有时在完全不同的含义下，被用于表示两样本t检验或独立样本t检验。

　　当存在三组或更多组数据集时，Prism提供嵌套单因素方差分析。我们使用该名称，是因为它最能描述此检验的用途：您想要比较三个或更多处理组，同时存在另一个需考虑的嵌套变量，但这并非主要目的。

　　其他书籍和程序在这两种情况下，通常使用嵌套双因素方差分析这一术语，原因是一个因素(如本例中的大鼠)嵌套于另一个因素(处理)之中。该分析需考虑两个因素(一个为嵌套因素)，故而得名嵌套双因素方差分析。

　　嵌套方差分析得另一个称谓是分层方差分析。

　　Prism如何执行嵌套t检验和单因素方差分析

　　Prism拟合混合效应模型。它将主因素(用于定义数据集列)视为固定因素，将嵌套因素视为随机因素。

　　若不存在缺失值，此分析得出的结果与仅将每个子列的均值用于分析的简单t检验或单因素方差分析结果完全一致。当存在缺失值时，则无此简便方式。

　　若P值大，是否应合并数据？

　　在嵌套t检验示例中，“大鼠(处理因素)”的P值为0.0239。按照统计学显著性的常规界定(P＜0.05)，您可拒绝“每个处理组内所有大鼠均值相同”这一原假设。

　　在嵌套单因素方差分析示例中，“牛群(处理因素)”的P值是0.1231。由于该值大于传统阈值0.05，您无法拒绝“每个处理组内所有牛群的平均红细胞压积相同”这一原假设。

　　因为P值“大”，是否就应判定牛群间无差异，进而合并数据并开展常规t检验呢？这是个难题：

　　这种做法的吸引力在于，均值差异的置信区间会更窄，且P值会更小。

　　问题在于，大P值并非证明(就本例而言)牛群均值完全相同，它仅说明您没有充足证据表明均值不同。

　　部分统计学家建议永远不要合并数据，认为合并本质上是为使主要比较的P值更低而耍的手段。还有些统计学家会谨慎建议合并，但仅在嵌套因素的P值相当大(比如大于0.25，甚至大于0.75)时才这样做。

　　Prism软件不便于进行数据合并操作，且我们也不推荐这样做。

　　嵌套t检验

　　操作方法：嵌套t检验

　　1.数据录入

　　这是Prism软件为嵌套t检验提供的教学数据。您要比较两种教学方法(数据集列)，每种方法在3个教室(子列)中使用，以每个教室4-6名学生的测量结果作为观测指标(行)。

　　若您不用教学数据，创建一个“嵌套表”，并将子列数量设置为与实际重复数对应。在本例中，每种教学方法用3个教室，所以创建有3个子列的表格。

　　录入数据时，把技术重复数据堆叠起来。在本例里，每个教室测量了4-6名学生，这些数据堆叠在每个子列中。在实验室示例中，您可能对3只大鼠(子列)应用每种不同处理，然后在每只大鼠上多次测量(技术重复，堆叠在子列中)。

　　若您想恰当标记子列(如下方的“教室1”……)，双击子列标题，调出对话框，在其中录入所有子列标题。

　　注意：

　　“技术重复”这一术语并非总是适用。若您研究每组中的三家医院，每家医院有四名医生，可将每家医院的信息堆叠在一个子列中，每名医生对应不同行。

　　注意，重复数据是堆叠的。这与Prism软件通常的操作方式不同。我们这样设置有两个原因。首先，它让您能够标记子列(如“教室1”、“教室2”……如上所述)。其次，它与大多数教材中进行此分析的方式一致。若您将技术重复数据(本例中的学生数据)与不同重复数据(本例中的教室数据)在不同行中并排录入，Prism的嵌套t检验分析会得出无意义的结果。

　　每个子列中数值的顺序是任意的。您可随机打乱每个子列中的数据，结果不会改变。第2行中的数据彼此完全不匹配。

　　子列的顺序无关紧要。若您交换“教室2”和“教室3”的数据，结果会相同。比如，对照数据的第二个子列和处理后数据的第二个子列之间并无关联。

　　在此示例中，注意子列的数值数量并不相同。嵌套t检验在样本量不等时也能正常运行。

　　我们使用“嵌套t检验”这一名称，因为它最贴切地描述了该检验的用途。大多数书籍将其称为嵌套双因素方差分析，原因是一个因素(本例中的“教室”)嵌套于另一个因素(教学方法)之中。

　　本示例源自Maxsell和Delaney所著书籍(第3版)的表18.4。他们将第二组的3个教室标记为1、2、3，而非4、5、6。这是因在SPSS中分析这些数据时存在特殊情况，数据间并无匹配关系。第一种教学方法对应的第二个教室(教室2)与第二种教学方法对应的第二个教室(我们称其为教室5，但书中也称作教室2)完全不匹配。

　　Prism软件无法对超大规模数据集执行嵌套t检验，若尝试，会弹出提示信息告知用户。多大规模算“超大”？

　　2.执行分析

　　点击“分析”，然后从“分组分析”列表中选择“嵌套t检验”。

　　在第一个选项卡中，录入两个因素的名称：

　　第二个选项卡提供以下选项：

　　第三个选项卡提供多种绘制残差图的选择。

　　结果解读：嵌套t检验

　　重要结果

　　-P值

　　结果呈现形式与非配对t检验类似。P值用于检验“两种处理均值相同”这一原假设。P值可通过t比值(对应t检验)或F比值(因这类数据常采用嵌套方差分析进行分析)计算得出。T比值是F比值的平方根(因分母自由度为0)，故无论用哪种方式计算，P值相同。我们同时展示两种结果，方便您与其他程序或文献的结果对应上。

　　-置信区间

　　最重要的结果是两均值差值的95%置信区间。若您需要，可在对话框中选择90%或99%置信区间。

　　其他结果(多数科学家会忽略的结果)

　　嵌套t检验拟合的是混合模型。称其为“混合”，是因为假设堆叠在子列中的数值以及子列的选择是随机的，而处理因素(本例中为教学方法)是固定的。这意味着我们关注对这两种教学方法的检验，但学校的选择以及学校内学生的选择是随机的。我们并不关注具体是哪些学生或哪些学校。该模型拟合子列内和子列间的变异，同时报告方差和标准差(标准差是方差的平方根)。Prism输出这些结果，以便您与其他程序或文献对比。不过这些数值的实用价值不高。

　　您将学生分到不同子列，是因为预期不同教室(场景)的结果会有差异。Prism检验的原假设是：实际上，同一列(教学方法)内的所有子列(学校)都是相同的。此处P值为0.0027，因此您可以拒绝该原假设。该检验的实用价值有限。

　　Prism可选择报告REML(限制性极大似然)拟合优度，以与其他程序和文献匹配。但尝试解读该指标并无实际意义。

　　嵌套t检验的另一个示例

　　示例数据

　　本示例分析的是先前展示的数据，涉及重复实验用的大鼠，每只大鼠有多次测量值(技术重复，指对同一实验对象的重复测量，用于评估检测的重复性和可靠性)。

　　嵌套t检验结果

　　对照组与处理组均值差异的95%置信区间为-2.3至15.9。用于检验“两个总体无差异”这一原假设的P值为0.11。这些数据无法为处理效应提供有说服力的证据。

　　用于检验“每一列内所有子列均相同”这一原假设的P值为0.0024。这为大鼠个体间存在差异提供了证据。

　　分析核对清单：嵌套t检验

　　嵌套t检验用于比较两组不匹配组别(非配对组)的均值，这些处理组内存在一个嵌套因素。

　　✅残差是否服从高斯分布(正态分布)？

　　嵌套t检验假定残差(很多情况下是技术重复间的变异)来自高斯分布的抽样。由于中心极限定理，在大样本时，该假定的影响较小。

　　嵌套t检验对话框的第三个选项卡，可让您通过多种方式绘制残差图，以评估其正态性。

　　✅每个子列内的变异是否具有相同方差？

　　嵌套t检验假定每个子列中的数据，来自具有相同标准差(相同方差)的总体。Prism不检验这一点，但您可查看数据，判断该假定是否被严重违背。

　　可考虑对数据的对数值进行方差分析。在某些情况下，这会使方差更接近相等。

　　✅子列均值间的变异是否呈高斯分布？

　　嵌套t检验假定子列均值间的变异呈高斯分布，且子列内的重复测量值也呈高斯分布。

　　✅您是否在比较恰好两组数据？

　　仅在比较两组数据时使用t检验。不宜多次进行嵌套t检验、每次仅比较两组处理组(的做法)。

　　✅两列是否均包含数据？

　　若您想将一组实验数据与理论值(比如100%)比较，请勿用该理论值填充一列后进行非配对t检验。而是应使用单样本t检验(one-samplettest)。

　　✅您是否确实想比较均值？

　　嵌套t检验用于比较两组的均值。即便分布存在大量重叠，也可能得到极小的P值(这是总体均值不同的明确证据)。在某些情况下(例如，评估诊断性检验的有效性)，相较于均值差异，您或许对分布的重叠情况更感兴趣。

　　嵌套单因素方差分析

　　操作方法：嵌套单因素方差分析

　　本示例源自优秀的在线统计教材《如何避免和发现统计舞弊》。该研究评估了两种病媒控制方法与不进行控制对牛红细胞压积(PCV)的影响。三头牛群被随机分配到三种处理中的每一种。从每头牛群的四头牛身上采集血液样本，并将红细胞压积制成表格。

　　1.数据录入

　　创建一个“嵌套表格”，并根据实际重复次数设置子列数量。在本示例中，每个处理组有3个牛群，因此创建一个含3个子列的表格。

　　将重复牛只的数据堆叠录入。

　　如需恰当标记子列(如下方的“牛群1”……)，双击子列标题，调处录入子列标题的对话框。

　　注意：

　　注意，重复样本是堆叠的。这与Prism软件通常的操作方式不同。我们这样设置有两个原因。首先，它让您可以标记子列(如上方的“牛群1”“牛群2”……)。其次，它与大多数教材进行该分析的方式一致。如果技术重复(如不同行中的大鼠)分布在不同行，Prism的嵌套t检验分析会给出无意义的结果。

　　每个子列中数值的顺序是任意的。您可以随机打乱每个子列中的数据，结果不会改变。第2行的数值彼此完全不匹配。

　　子列的顺序无关紧要。如果您交换牛群2和牛群3的数据，结果会相同。比如，处理组数据的第二子列和对照组数据的第二子列之间没有关联。

　　在本示例中，每个子列的数值数量(样本量)相同(均为4)。嵌套单因素方差分析不要求这一点，样本量不等时也能正常运行。

　　我们使用“嵌套单因素方差分析”这一名称，因为它最能描述该检验的用途。大多数教材称其为嵌套双因素方差分析，因为一个因素(本例中的牛群)嵌套于另一个因素(处理)之中。

　　Prism软件无法对超大数据集运行嵌套方差分析。

　　2.运行分析

　　点击“分析”，然后从“分组分析”列表中选择“嵌套单因素方差分析”。

　　在第一个选项卡，选择是否为每个数据集生成总均值和95%置信区间的图形，以及是否在表格结果中显示拟合优度。

　　第二个选项卡提供多重比较的选项，第三个选项卡给出绘制残差的若干选择。

　　结果解读：嵌套t检验

　　主要结果

　　嵌套方差分析：此P值用于检验“三列(本例中为不同处理)的均值总体相同”这一原假设。

　　随机效应：子列均值间及子列内的变异，以标准差(对科研人员更易理解)和方差(对统计学家更熟悉)两种形式呈现。

　　子列是否存在差异：该P值检验“所有子列的数据均来自标准差相同的总体”这一原假设。

　　拟合优度(可选)：若您选择此选项，Prism会报告自由度(df)数量和REML准则(REMLcriterion)，这仅对熟悉混合模型的统计学家有意义。

　　多重比较

　　多重比较的执行方式与单因素方差分析一致。就本例而言，用邓尼特检验将两种处理与第三列的对照组比较是合理的，以下是结果。

　　分析核对清单：嵌套单因素方差分析

　　嵌套单因素方差分析用于比较三组或更多组不匹配组别(非配对组)的均值，这些处理组内存在一个嵌套因素。

　　✅残差是否服从高斯分布(正态分布)？

　　嵌套方差分析假定残差(很多情况下是技术重复间的变异)来自高斯分布的抽样。由于中心极限定理，在大样本时，该假定的影响较小。

　　嵌套t检验对话框的第三个选项卡，可让您通过多种方式绘制残差图，以评估其正态性。

　　✅每个子列内的变异是否具有相同方差？

　　嵌套方差分析假定每个子列中的数据，来自具有相同标准差的总体。Prism不检验这一点，但您可查看数据，判断该假定是否被严重违背。

　　可考虑对数据的对数值进行方差分析。在某些情况下，这会使方差更接近相等。

　　✅子列均值间的变异是否呈高斯分布？

　　嵌套单因素方差分析假定子列均值间的变异呈高斯分布，且子列内的重复测量值也呈高斯分布。

　　✅您是否确实想比较均值？

　　嵌套方差分析用于比较三组或更多组的均值。即便分布存在大量重叠，也可能得到极小的P值(这是总体均值不同的明确证据)。在某些情况下(例如，评估诊断性检验的有效性)，相较于均值差异，您或许对分布的重叠情况更感兴趣。

　　✅主因素是“固定因素”而非“随机因素”吗？

　　Prism假定组别(数据集)是固定因素。换言之，Prism检验您所采集数据的特定组别间均值是否存在差异。组别(数据集)也可能代表随机因素，比如当您从无限(或至少大量)可能的组别中随机选取组别，且希望得出关于所有组别(包括未纳入本实验的组别)差异的结论时。若主因素是随机因素，Prism无法执行嵌套方差分析。

　　注意：Prism假定嵌套因素是随机因素。

　　✅不同列是否代表分组变量的不同水平？

　　嵌套单因素方差分析用于探究单一变量在三组或更多组间是否存在显著差异。在Prism中，您需将每个组录入单独一列。若不同列代表不同变量(而非不同组别)，则单因素方差分析并非合适的分析方法。例如，若A列是葡萄糖浓度、B列是胰岛素浓度、C列是糖化血红蛋白浓度，单因素方差分析就不适用。

上一条：SnapGene 预测开放阅读框ORFs

下一条：SnapGene怎么用