Minitab 数据非正态如何分析？您可能问了错误的问题！

统计学为分析实际生产中常见的数据提供了有用的分析方法，评估这些数据有助于做出正确而有益的决定。通过一种有组织的方法来评估观察到的数据，它可以帮助研究人员避免得出错误结论，并做出对产品的质量不明智甚至危险的判断。

统计为面对不确定性时的决策提供方法和工具，我很喜欢统计学家C.R.劳先生的一句话“在理性的世界里，所有的判断都是统计”，甚至把它作为我微信的个性签名。

我虽然很钟爱统计学，但我不是盲目的信徒，因为平常分析时马克吐温有一句名言经常在我脑中回荡：“世界上有三种谎言：谎言，该死的谎言，以及统计数据。”这句名言是有道理的，下面我以“正态分布”为例来说明我的观点。

正态分布 为何如此重要

作为Minitab技术支持，我很欣慰我的学员和客户问我一个问题：老师，我的数据非正态，我该如何分析？正如本文标题所言，这是一个错误的问题，但仍然令我欣慰，为什么呢？因为当您问到这个问题的时候，说明在分析的时候做了思考。很多统计工具和质量工具在使用时都有严格的前提条件需要满足，其中之一就是——数据必须服从正态分布。

比如说，我们在使用以下常用质量工具和统计工具时，需要满足正态要求：

1. 控制图

2. 过程能力分析

3. 单t、双t、配对t检验等

4. 方差分析

5. 残差分析

为什么说这是一个错误的问题

正态数据做分析上手很快，但世事无常，我们经常面临的数据都是非正态，下面我们以过程能力分析为例。

能力分析之前需要做正态检验，这一点从过程能力指数的公式中大家应该都明确。

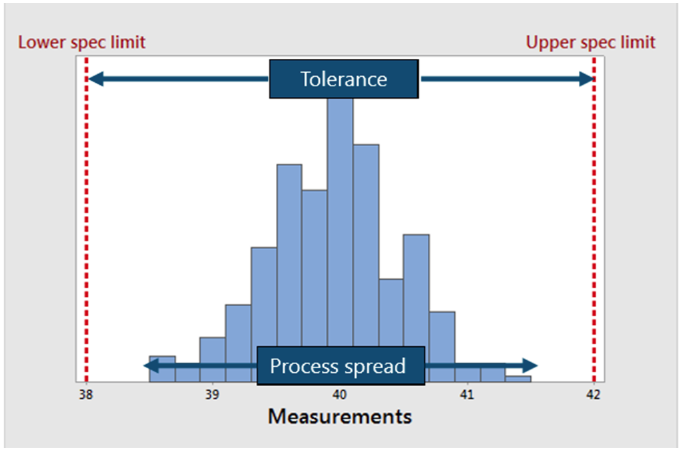
用6σ作为过程变异的度量-要求正态性。

随着质量人员统计意识的提高，对于能力分析之前先做正态性检验，大家基本没问题。

误区

关键的问题是，如果正态性检验后发现数据非正态了，该如何去处理？这时候，很多同学首先想到的办法就是转换数据分布，把非正态数据转换成服从正态分布的数据，对吗？

过程能力 分析案例

为了防止工具的滥用，我们通过一个具体的案例来进一步说明。假如，我们现在想对某一药品的有效成分含量进行过程能力分析，规格下限360mg/ml，规格上限370mg/ml，数据如下：

正如前面所言，过程能力分析先做正态性检验，我们来看一下正态性检验结果：

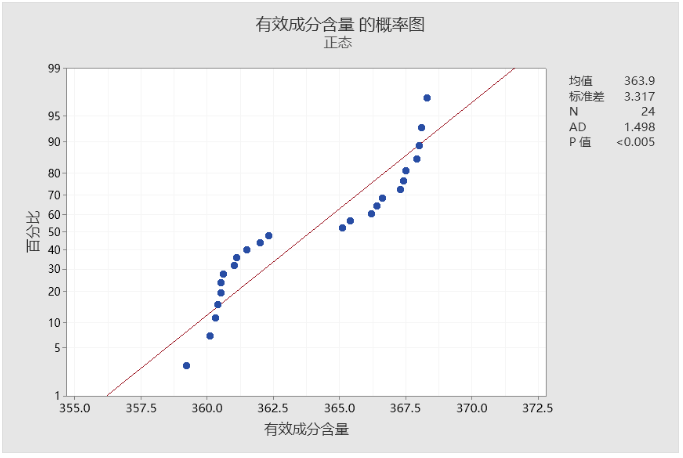
有效成分含量正态性检验的P值小于0.005，那它肯定比0.05要小，故数据非正态。其实，我们之前总结了能力分析的一些思路（如下图）：

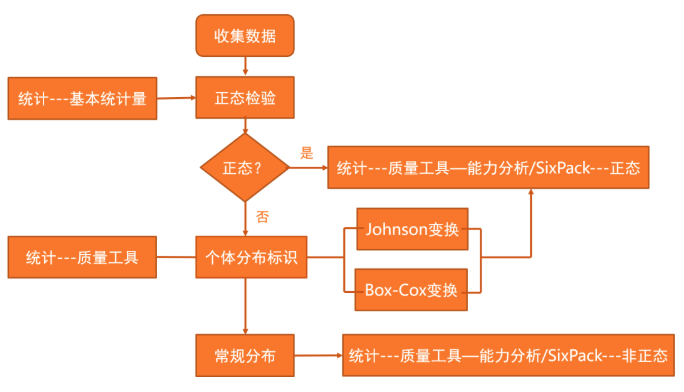
但数据非正态，不要急着转换数据，先做一个“个体分布标识”看看转换合适，还是用非正态方法合适。那我们来看一下个体分布标识的结果：

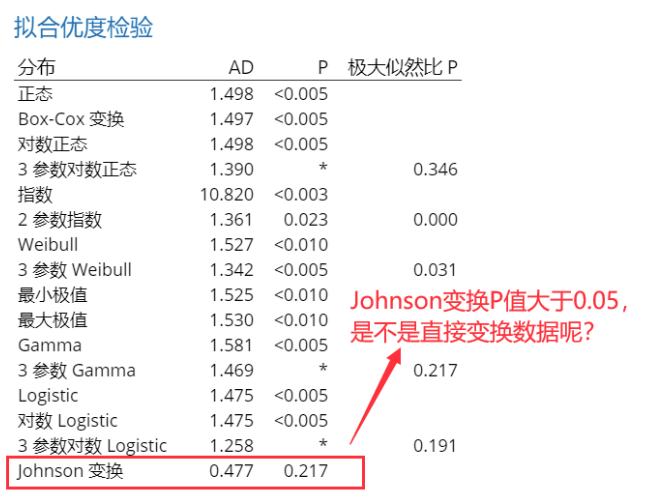
恭喜您，在个体分布标识的拟合优度检验中找到一个P值大于0.05的变换方法——Johnson变换。有些学员分析到这里很激动，终于找到解决非正态的处理办法了，直接用上面给出的Johnson变换函数变换数据做过程能力分析。

不要忘记使用 可视化分析

根据上面的操作步骤，您可能会得到一个很好看的能力报告，但殊不知从一开始就问了错误的问题——非正态数据如何分析？

那正确的问法是什么呢？其实对于非正态分析问题，正确的问法应该是：

数据为什么非正态?

生产中很多指标，根据形成机理来看，可能有很多应该是近似服从正态分布的，如案例中的有效成分含量。那么现在为什么非正态呢？要想解决这种问题，需要我们基于现场，追溯数据来源。通过分析，最终发现当前收集到的有效成分含量数据其实是来源于两个不同的工艺条件：130℃和150℃，但是分析的时候把它们混在了一起，结果导致数据非正态。我们来看一下，最终的数据格式。

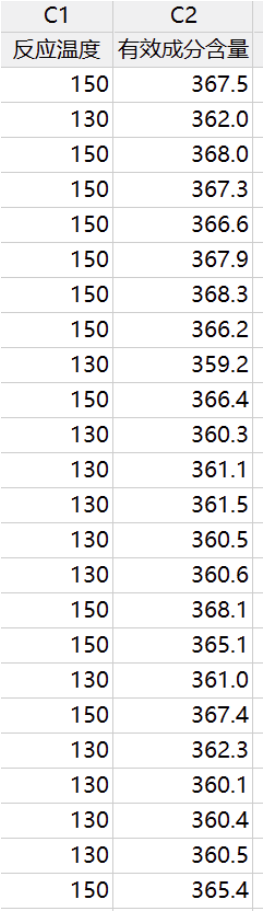
用图形化汇总，分别对两种温度下数据做正态性检验，结果都是服从正态分布：

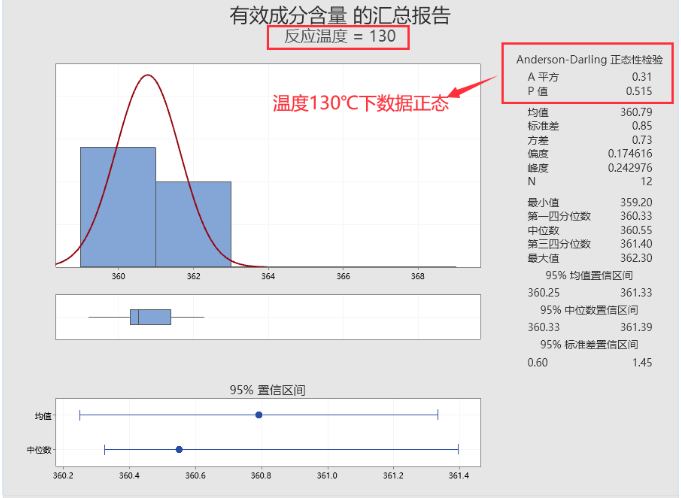
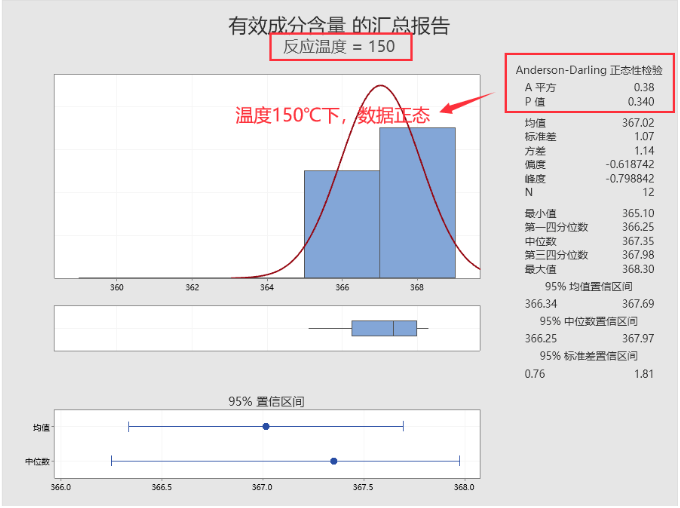
如果针对此数据做一次双样本t检验，您还会发现130℃和150℃下，有效成分含量存在显著差异，或者说这是来自两个总体的数据，但现在您却把它们混在了一起来做分析。

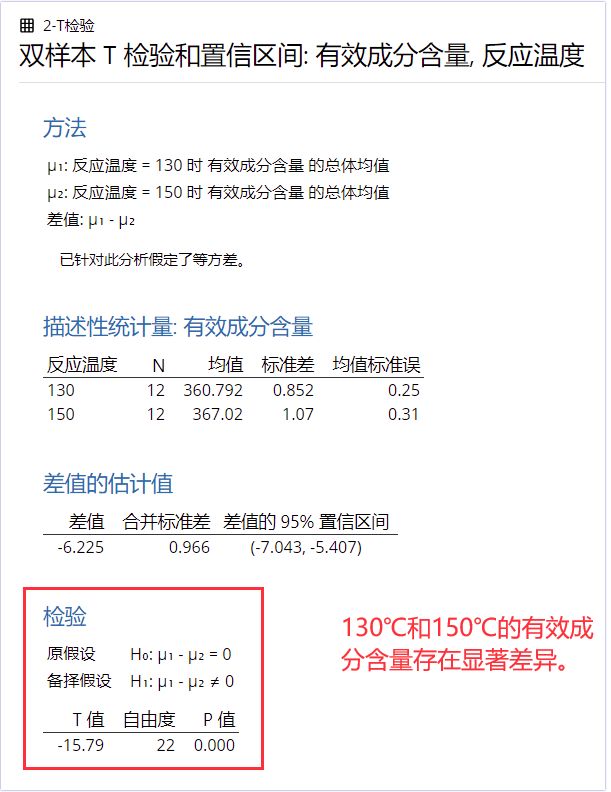
至此，我们问了正确的问题，并得到了关于数据为什么非正态的答案：由于把有显著差异的两个总体130℃和150℃的数据混在了一起，导致数据出现双峰（如下图），最终无法通过正态性检验。

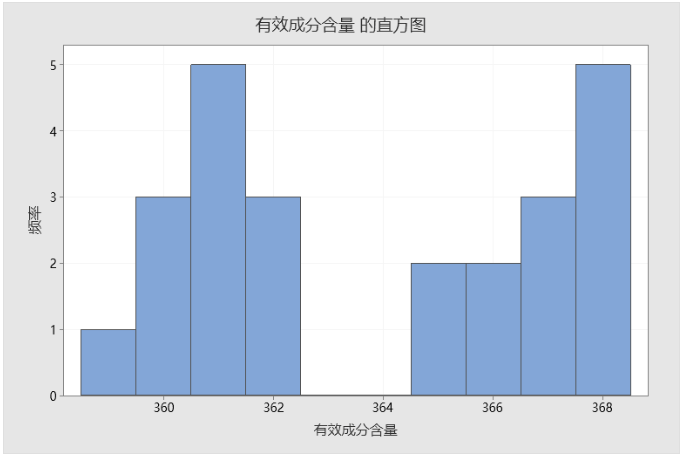
不要去纠结非正态数据该如何处理，望前看，去找非正态的原因才是统计的正确打开方法。有人可能会说，原因不好找！确实，如果您的数据记录不完整，无法追溯，您可能不知道原因出在哪里，有可能是两个批次的混在一起，也有可能是不同班次……

找原因的时候，统计方法能帮助您去确定一些问题，如上面的双样本t检验证实这是来自两个不同总体的数据，不能混在一起。但是请记住，我们的工艺经验也很重要，比如上面案例中发现是工艺条件不同（130℃和150℃）。

请记住，丰富的经验可以让你成为一个工程师，但如果结合统计分析，您可能将会成为一个更好的工程师。

上一条：Minitab|没有失效或失效很少的可靠性分析-Weibayes分析

下一条：SketchUp缩略图不显示了怎么办？